Post-hoc testid

Juhul, kui dispersioonanalüüsi tulemus ütleb, et faktori mõju on statistiliselt oluline, kerkib sageli järgmine küsimus: millised võrreldud gruppidest on omavahel statistiliselt oluliselt erinevad? Taolisi, statistiliselt oluliseks osutunud dispersioonanalüüsi järgselt teostatud teste nimetatakse post-hoc testideks ning levinud on need eelkõige täpselt planeeritud ja läbi viidud katsete puhul (põldkatsed, söötmiseksperimendid jne).

Enam levinud post-hoc testid on Fisheri LSD (Least Significant Difference), Tukey, Scheffe ja Sidaki test. Mitte ühtki neist ei leidu Exceli statistilise analüüsi vahendite hulgas. Aga teades testide arvutuseeskirju ja vajadusel ka tabeleid kriitiliste väärtuste arvutamiseks, on nende testide teostamine Excelis võimalik.

Järgnevalt on näidatud, kuidas viia Excelis läbi kõige lihtsam post-hoc test - Fisheri LSD test.

Fisheri LSD testi puhul arvutatakse nn vähim oluline vahe, so vähim gruppide vaheline erinevus, mille võib veel lugeda statistiliselt oluliseks, valemist

,

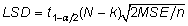kus k on võrreldavate gruppide arv (faktori tasemete arv), n on võrreldavate gruppide suurus, N = nk on vaatluste arv, MSE on jääkidele vastav keskruut dispersioonanalüüsi tabelist ning t_1-α/2(N - k) on t-jaotuse kvantiil (protsendipunkt) kohal 1-α/2 vabadusastmete arvuga N - k, mis Excelis on leitav funktsiooniga T.INV.2T (argumentideks olulisuse nivoo α ja N - k).

Seega tuleb Fisheri LSD testi teostamiseks Excelis

1. viia läbi ühefaktoriline dispersioonanalüüs,
2. arvutada välja vähima olulise vahe LSD väärtus ja
3. võrrelda kõigi gruppide paarikaupa erinevusi LSD-ga:

• kui kahe grupi keskmiste vaheline erinevus < LSD, siis ei ole võrreldud grupid statistiliselt oluliselt erinevad,
• kui kahe grupi keskmiste vaheline erinevus >= LSD, siis on võrreldud grupid statistiliselt oluliselt erinevad.

Joonisel 70 on näidatud nelja kartulisordi saagikuse võrdlemist ühefaktorilise dispersioon-analüüsiga ja selle järgselt Fisheri LSD testiga. Vähima olulise vahe LSD väärtuse arvutamiseks on kasutatud dispersioonanalüüsi tabelis sisalduvaid suuruseid, keskmiste paarikaupa võrdluste tarvis on tehtud abitabel, kuhu on esmalt välja arvutatud kõik keskmiste paarikaupa erinevused ning seejärel on neid erinevusi võrreldud vähima olulise vahe LSD väärtusega (kirjutades tärni statistiliselt oluliste erinevuste järele).

Märkus. Kui võrreldavad grupid on erineva suurusega, tuleb iga paariviisilise võrdluse tarvis arvutada oma LSD väärtus valemist

,

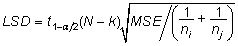kus n_i ja n_j on mõõtmiste arvud võrreldavates gruppides i ja j.

NB! Fisheri LSD test ei korrigeeri tulemusi mitmese testimise suhtes, st et kõigi paariviisiliste võrdluste peale kokku on tõenäosus, et mõni erinevus on ilmenud lihtsalt juhuslikult, suurem kui 0,05.
 

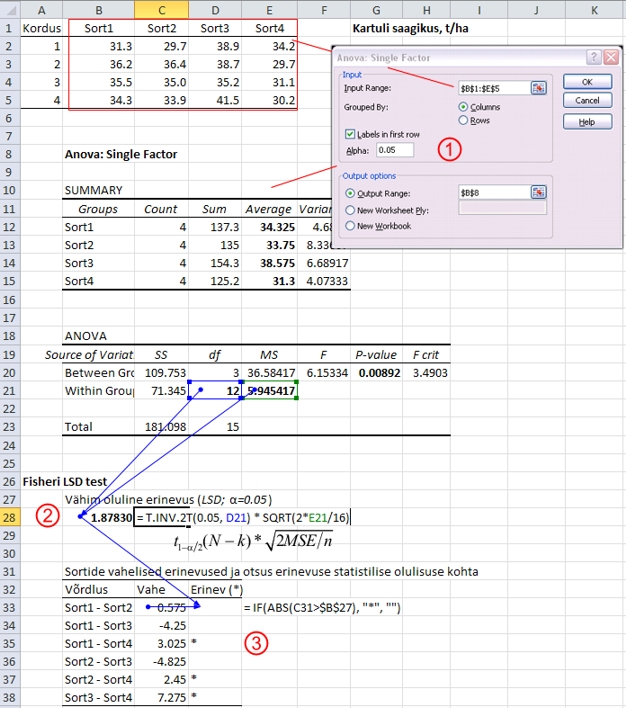
Joonis 70. Nelja kartulisordi saagikuse võrdlemist ühefaktorilise dispersioonanalüüsiga ja selle järgselt Fisheri LSD testiga.