|
Usalduspiirid
keskmisele
Keskmise
usalduspiiride leidmine funktsioonide abil
Üldine
valem mingi parameetri hinnangu usalduspiiride leidmiseks
on kujul:
parameetri
hinnang ± (tabeli väärtus * parameetri
hinnangu standardviga).
Nn
tabeli väärtus kujutab enesest mingi teoreetilise
jaotuse protsendipunkti ning see sõltub nii
ette antud protsendist kui ka hinnatava parameetri
teoreetilisest jaotusest.
Mõnikord
on viimase valikuks mitu võimalust. Näiteks
juhul, kui uuritava tunnuse varieeruvus (dispersioon)
on teada või on tegu suure valimiga, on keskmise
usaldusintervall leitav standardse normaaljaotuse
alusel valemist
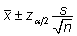 . .
Kui
aga varieeruvust teada pole ja valim on väike,
tuleb kasutada veidi "raskemate sabadega"
t-jaotust (sest tuleb arvestada ka dispersiooni hindamisel
tekkinud võimaliku veaga, mis omakorda muudab
keskmise hinnangu ebatäpsemaks ja seda eriti
väikese valimi korral):
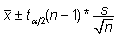 . .
Excelis
ongi keskmise usalduspiiride arvutamiseks kaks eraldi
funktsiooni: CONFIDENCE.NORM ja CONFIDENCE.T.
Mõlemad
funktsioonid tahavad argumentidena ette (Joonis 25)
- olulisuse
nivood Alpha (95%-lise usaldusintervalli
korral on olulisuse nivoo 0,05),
- uuritava
tunnuse standardhälvet või selle hinnangut
Standard_dev (vastavalt funktsiooni CONFIDENCE.NORM
või CONFIDENCE.T puhul, leituna funktsioonidega
STDEV.P või STDEV.S),
- vaatluste
arvu Size.
NB!
Funktsioonide CONFIDENCE.NORM või CONFIDENCE.T
tulemusena saadud arv näitab usalduspiiride kaugust
keskväärtusest (poolt usaldusintervalli
laiusest), usalduspiiride eneste leidmiseks tuleb
see siis kas liita või lahutada aritmeetilisest
keskmisest (Joonis 26).
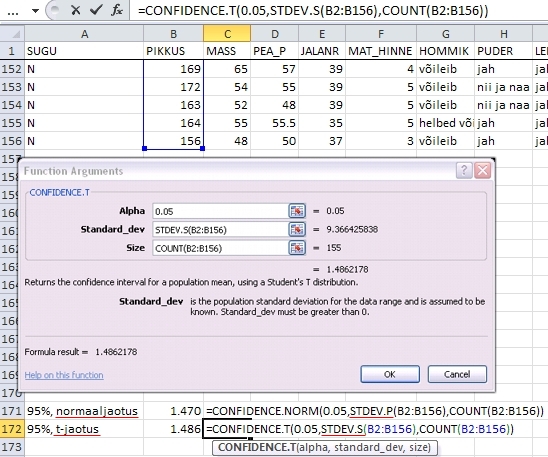
Joonis
25. Usalduspiiride arvutamine tudengite keskmisele
pikkusele funktsioonidega CONFIDENCE.NORM ja CONFIDENCE.T.
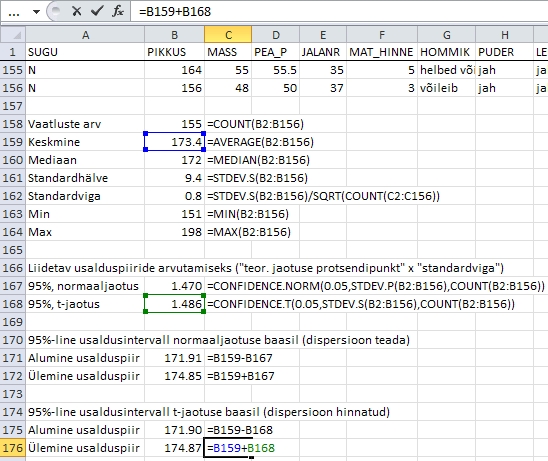
Joonis
26. Usalduspiiride arvutamine tudengite keskmisele
pikkusele funktsioonide CONFIDENCE.NORM ja CONFIDENCE.T
tulemuste ning aritmeetilise keskmise alusel.
Tulemustest
nähtub, et tudengite keskmine pikkus jääb
95%-lise tõenäosusega vahemikku 171,9-174,9
cm. Seejuures on normaaljaotuse baasil hinnatud usaldusintervall
vaid õige pisut kitsam, sest valim on piisavalt
suur (n=155) garanteerimaks ka hinnangute täpsust.
Märkus.
Ekslikult väidab Excel ka funktsiooni CONFIDENCE.T
tellimisaknas ja abifailis, et funktsiooni argumendina
ette antav standardhälve on populatsiooni teadaolev
standardhälve. Tegelikult on see väide õige
vaid funktsiooni CONFIDENCE.NORM puhul, funktsiooni
CONFIDENCE.T rakendamisel eeldatakse ikka, et populatsiooni
standardhälve ei ole teada ja on seetõttu
andmetest hinnatud (funktsiooniga STDEV.S).
Keskmise
usalduspiiride leidmine protseduuriga Descriptive
Statistics
Kui
uuritava tunnuse dispersioon ei ole teada (ja nii
see tavaliselt on), on keskväärtuse usalduspiiride
leidmiseks lisaks funktsioonile CONFIDENCE.T kasutatav
ka protseduuri Descriptive Statistics valik
Confidence Level for Mean.
Tellimusakna
täitmine kulgeb analoogselt arvkarakteristikute
leidmisel kirjeldatuga (Joonis 21 peatükis
3.2), lisaks võib muuta usaldusnivood (vaikimisi
on selleks 95%).
Tulemusena
väljastatakse arvkarakteristikute tabelis suurus,
mis näitab uuritava tunnuse keskmise väärtuse
kaugust oma alumisest ja ülemisest usalduspiirist
(poolt usaldusintervalli laiust). Usalduspiirid leitakse,
liites ja lahutades saadud arvu tunnuse aritmeetilisele
keskmisele (Joonis 27).
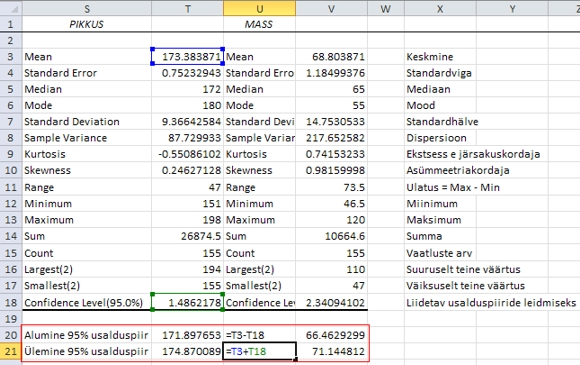
Joonis
27. Usalduspiiride arvutamine tudengite keskmisele
pikkusele ja kehamassile protseduuri Descriptive
Statistics poolt väljastatud tulemuste alusel.
|