Usalduspiirid teistele parameetritele

Et Excelis on olemas funktsioonid mitmete erinevate teoreetliste jaotuste kvantiilide e protsendipunktide leidmiseks, on usalduspiirid leitavad ka otse vastavaid valemeid Excelis rakendades.

Usalduspiirid keskmisele

Eelmises punktis kirjeldatud usalduspiirid keskmisele võinuks leida ka otse lähtuvalt valemeist

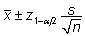või .

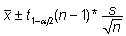Suurused 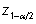ja 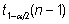neis valemeis on vastavalt standardse normaaljaotuse ja vaatluste arvule n vastava t-jaotuse 1-α/2-kvantiilid (väärtused, millest suuremaid väärtuseid saab antud jaotuse korral olla vaid α/2*100%). 95%-lise usaldusintervalli korral on olulisuse nivoo α = 0,05 ja arvutusteks tuleb leida kas standardse normaaljaotuse või t-jaotuse 97,5%-punkt ehk (1 - 0,05/2) = 0,975-kvantiil. Leitavad on need kvantiilid vastavalt funktsioonidega NORM.S.INV ja T.INV.

Tudengite keskmise pikkuse 95%-liste usalduspiiride arvutamine, lähtudes otse usalduspiiride valemeist, on esitatud joonisel 28.

Tulemustest nähtub, et tudengite keskmine pikkus jääb 95%-lise tõenäosusega vahemikku 171,9-174,9 cm. Seejuures on normaaljaotuse baasil hinnatud usaldusintervall vaid õige pisut kitsam, sest valimi on piisavalt suur (n = 155) garanteerimaks ka ligikaudsete hinnangute täpsust.
 

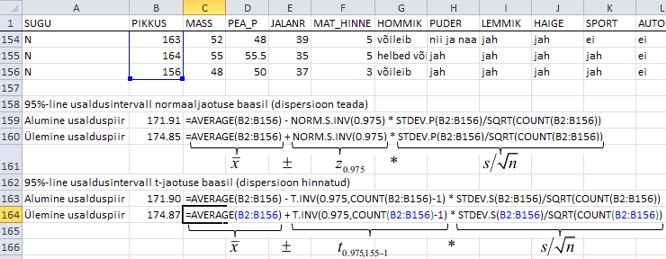
Joonis 28. Usalduspiiride arvutamine tudengite keskmisele pikkusele Exceli funktsioonide abil lähtudes otse usalduspiiride valemeist.
 

Usalduspiirid protsendile

Suure valimi (enamasti tähendab see, et n>60) korral on protsendi usaldusintervalli arvutamiseks kasutatav juba keskväärtuse usaldusintervalli arvutamisest tuttav valem

,

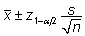kus aritmeetiline keskmine tähendab hinnangut uuritava sündmuse toimumise tõenäosusele, 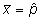, ja standardhälve avaldub vastavalt binoomjaotusele kujul .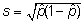

Seega on uuritava sündmuse toimumise tõenäosuse usaldusintervall leitav valemist

.

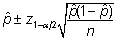Usaldusintervalli protsendile saab, kui korrutada eelmine avaldis 100%-ga.

Joonisel 29 on näidatud 95%-lise usaldusintervalli arvutamist õlut joovate tudengite osakaalule. Tulemustest nähtub, et hinnanguliselt 36,1% tudengitest joob õlut, kusjuures 95%-lise tõenäosusega jääb õlut joovate tudengite protsent vahemikku 28,6-43,7%.
 

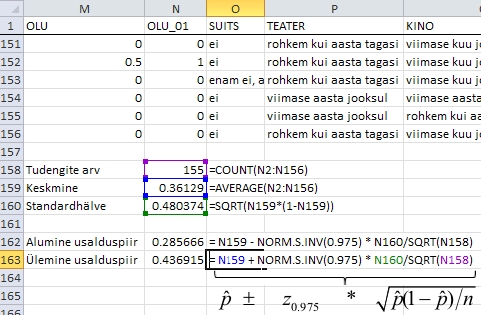
Joonis 29. Usalduspiiride arvutamine õlut joovate tudengite osakaalule Exceli funktsioonide abil lähtudes otse usalduspiiride valemeist.
 

Usalduspiirid dispersioonile

Normaaljaotusega tunnuse dispersiooni alumine ja ülemine usalduspiir leitakse vastavalt valemeist

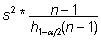ja ,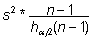

kus s² on valimi dispersioon, n on vaatluste arv ning 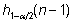ja 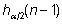on hii²-jaotuse kvantiilid vabadusastmete arvu n - 1 korral. Excelis on viimased leitavad funktsiooniga CHISQ.INV.

Standardhälbe alumine ja ülemine usalduspiir leitakse vastavalt valemeist

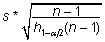ja .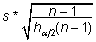

Joonisel 30 on näitatud 95%-lise usaldusintervalli arvutamist tudengite pikkuse standard-hälbele. Tulemustest nähtub, et 95%-lise tõenäosusega jääb tudengite pikkuse standardhälve vahemikku 8,4-10,5 cm.
 

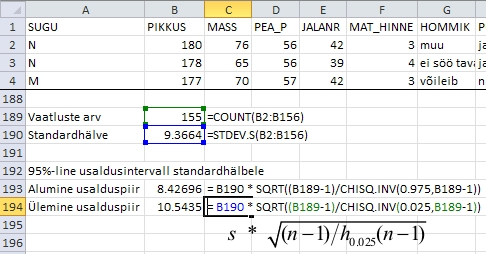
Joonis 30. Usalduspiiride arvutamine tudengite pikkuse standardhälbele.