Lineaarse korrelatsioonikordaja statistiline olulisus

Korrelatsioonikordaja r statistilise olulisuse kontrollimine seisneb hüpoteeside paari

H₀: r = 0
H₁: r ≠ 0

testimises.

Kahjuks ei väljasta Excel korrelatsioonanalüüsi läbi viies automaatselt taoliste hüpoteeside kontrollimiseks vajalikke näitajaid (korrelatsioonikordaja või teststatistiku kriitilist väärtust või olulisuse tõenäosust p). Lahendusena tuleb kõne alla vähemalt kolm varianti.

Esiteks võib kasutada korrelatsioonikordajate kriitiliste väärtuste tabelit, mis on leitav enamuse statistikaõpikute lisades ja ka näiteks veebiaadressilt http://www.eau.ee/~ktanel/VL_0435/critical_values_of_Pearson_cor.pdf - kui leitud korrelatsioonikordaja väärtus on suurem vastavast kriitilisest väärtusest (viimane sõltub kordaja arvutamisel kasutatud väärtuste paaride arvust n ja olulisuse nivoost α), võib lugeda tõestatuks alternatiivse hüpoteesi H₁: korrelatsioonikordaja on nullist erinev ehk seos on statistiliselt oluline, vastasel juhul peab jääma nullhüpoteesi juurde.

Teine võimalus uuritava lineaarse seose statistilise olulisuse kontrollimiseks on teostada kahe uuritava tunnusega tavaline lineaarne regressioon protseduuri Regression abil. Lineaarse regressiooniseose statistilist olulisust iseloomustav olulisuse tõenäosus p kehtib ka lineaarse korrelatsioonikordaja jaoks (täpsemalt vt peatükk 7.1).

Kolmas võimalus on leida olulisuse tõenäosuse p väärtus tuginedes teststatistikule

,

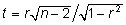mis on nullhüpoteesi kehtides ligikaudu t-jaotusega parameetriga n - 2.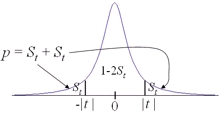

Otsuse, kumb hüpoteesidest on õige, vastu võtmiseks vajalik olulisuse tõenäosus p kujutab enesest leitud teststatistiku väärtuse poolt ära lõigatud t-jaotuse sabade osakaalu (kõrvaloleval joonisel pindalade S_t summa).

Excelis on p-väärtus leitav funktsiooniga T.DIST.2T, kus esimesena argumendina tuleb ette anda eelnevalt toodud teststatistiku absoluutväärtus ja teise argumendina korrelatsioonikordaja arvutamisel kasutatud väärtuste paaride arv n - 2.
Kui leitud olulisuse tõenäosus p < 0,05, võib lugeda kahe tunnuse vahelise seose statistiliselt oluliseks.

Joonisel 46 on esitatud noormeeste pikkuse ja kehamassi vahelise lineaarse korrelatsiooni-kordaja statistilise olulisuse testimine, kus vahetulemustena on välja kirjutatud ka vaatluste arv n ja teststatistiku absoluutväärtus |t|.

Tulemustest võib järeldada, et noormeeste pikkuse ja kehamassi vahel on keskmise tugevusega positiivne statistiliselt oluline seos (r = 0,46, p < 0,001).
 

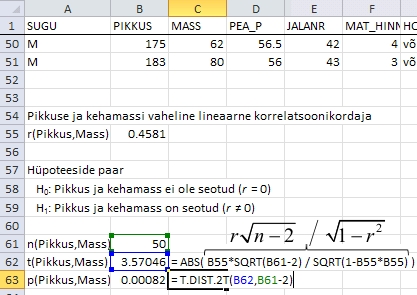
Joonis 46. Noormeeste pikkuse ja kehamassi vahelise lineaarse korrelatsioonikordaja statistilise olulisuse testimine.
 

Juhul, kui olulisuse tõenäosuseid soovitakse arvutada tervele korrelatsioonikordajate maatriksile (leituna protseduuriga Correlation), on mugav koondada arvutused analoogsesse tabelisse:

1. teha korrelatsioonikordajate tabelist koopia ja kustutada ära kopeeritud tabeli sisu (et ka hiljem oleks selge, mis arvud mis tabelis on, võib korrelatsioonikordajate ja loodava p-väärtuste tabeli ülemisse vasakusse nurka kirjutada vastava kordaja nime),
2. sisestada p-väärtuste tabeli lahtrisse valem olulisuse tõenäosuse arvutamiseks (Joonis 47),

   a) andes argumendina ette vastava korrelatsioonikordaja eelmises tabelis (lahtri aadressina) ja
   b) vaatluste arvu kas viitena seda sisaldavale lahtrile (NB! siis peab selle lahtri aadress olema fikseeritud) või lihtsalt arvuna ning
   c) lisades soovi korral valemi algusesse tingimuse funktsiooniga IF, mis juhul, kui korrelatsioonikordajate tabelis on arv 1 (peadiagonaalil) või mitte midagi (ülalpool peadiagonaali), jätab vastavad lahtrid p-väärtuste tabelis tühjaks,

3. kopeerida sisestatud valem kõigisse p-väärtuste tabeli lahtritesse.

NB! Kui arvutustes kasutatud vaatluste arv n on erinevate korrelatsioonikordajate puhul erinev (puuduvate väärtuste arv erinevatel tunnustel ja nende paaridel on erinev), tuleks enne p-väärtuste tabeli konstrueerimist teha analoogse struktuuriga tabel ka vaatluste arvude n tarvis ning kasutada p-väärtuste arvutamisel konktreetsele tunnuste paarile vastavat vaatluste arvu sellest tabelist.
 

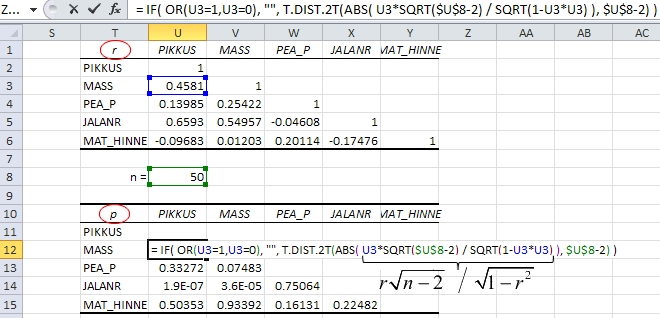
Joonis 47. Olulisuse tõenäosuste maatriksi arvutamine korrelatsioonikordajate maatriksi alusel.