Mitteparameetrilised testid

Juhul, kui uuritav tunnus ei ole normaaljaotusega ja valimi maht ei ole ka suur, ei ole Excelis olemas olevate z- ja t-testi rakendamine keskmiste võrdlemiseks korrektne (nagu ei ole korrektne ka dispersioonide võrdlemine F-testiga) ning kasutada tuleks mitteparameetrilisi normaaljaotust mitte-eeldavaid teste. Viimaste teostamiseks Excelis sisseehitatud vahendid puuduvad.

Siiski on mõnede mitteparameetriliste testide läbiviimine Excelis võimalik - kas siis testide aluseks olevate arvutuste samm-sammulise teostamise või spetsiaalsete lisamoodulite abil.

Märgitest funktsiooni BINOM.DIST abil

Näitena testi samm-sammulisest teostamisest on järgnevalt tutvustatud lihtsaima kahe sõltuva valimi võrdlemisel kasutatavat testi - märgitesti.

Kuna andmete näol on tegu sõltuvate (paaris) valimitega, saab iga indiviidi/objekti tarvis leida toimunud muutuse suuruse.

Märgitest

• loeb kokku, kui mitme indiviidi/objekti puhul üldse mingi muutus toimus (n₀) ja
• kui mitmel juhul oli muutus positiivne (miinusmärgiga, N₊) ja/või negatiivne (miinus-märgiga, N_-), ning
• leiab, tuginedes binoomjaotusele B(n₀, 0,5), kui suure tõenäosusega võinuks nii suur hulk samasuunalisi muutusi olla toimunud juhuslikult (juhusliku muutumise korral peaks iga indiviidi/objekti puhul olema nii positiivse kui ka negatiivse muutuse tõenäosus 0,5 - sellest ka binoomjaotuse teise parameetri väärtus).

Märgitesti teostamiseks (st olulisuse tõenäosuse p arvutamiseks) Excelis tuleb (Joonis 40)

1. leida kõigi väärtustepaaride vahed,
    
2. lugeda kokku, kui mitmel juhul on uuritava tunnuse väärtus muutunud ning kui mitmel juhul oli muutus positiivne (ja/või negatiivne),
    
3. rakendada funktsiooni BINOM.DIST, millele tuleb ette anda

• positiivsete või negatiivsete muutuste arv N₊ või N_- (Number_s),
• kõigi toimunud muutuste arv n₀ (Trials),
• positiivse muutuse toimumise tõenäosus nullhüpoteesi eeldusel, so 0,5 (Probability_s),
• väärtus TRUE argumendile Cumulative (siis väljastab funktsioon BINOM.DIST nii antud muutuste arvu kui ka sellest vähemtõenäoliste muutuste arvu summaarse tõenäosuse; väärtuse FALSE puhul on tulemuseks vaid antud muutuste arvu tõenäosus - vt ka Joonis 41).

Et funktsiooni BINOM.TEST tulemuseks argumendi Cumulative väärtuse TRUE puhul on vaid ühepoolsele hüpoteesile vastav olulisuse tõenäosus p, tuleb standardse kahepoolsele hüpoteesile vastava p-väärtuse saamiseks funktsiooni BINOM.TEST tulemus korrutada kahega (Joonised 40 ja 41).

Joonisel 40 esitatud märgitesti tulemusest nähtub, et tudengite testi tulemused enne ja pärast kursuse läbimist ei ole statistiliselt oluliselt erinevad (p = 0,18). Tulemus on erinev peatüki 5.5 alguses t-testiga leitust (Joonis 37), kus p-väärtus tuli 0,020. Põhjus on märgitesti robustsuses võrreldes t-testiga - t-test eeldab andmete normaaljaotuse-järgset jaotumist, märgitesti puhul on eelduseks vaid uuritava tunnuse väärtuste järjestatavus, lisaks ei arvesta märgitest toimunud muutuste suurusega.
 

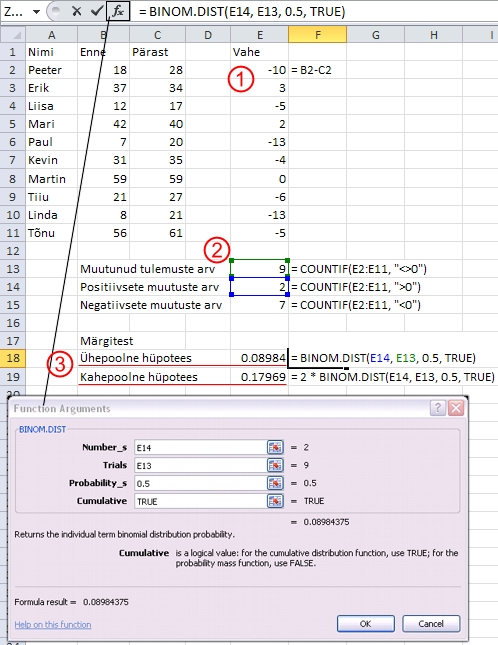
Joonis 40. Märgitest Excelis funktsiooni BINOM.DIST abil.
 

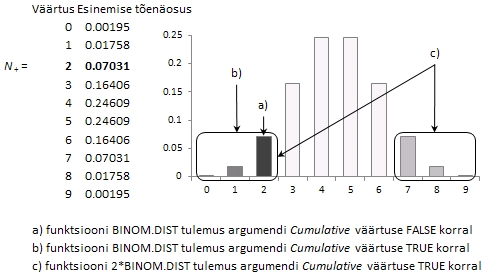
Joonis 41. Funktsiooni BINOM.DIST tulemus sõltuvalt argumendi Cumulative väärtusest.
 

Lisamoodul "Kahe üldkogumi võrdlus"

Aastal 2005. kaitses Anu Iher Tartu Ülikooli matemaatilise statistika instituudis bakalaureusetöö "Olulisemad kahe üldkogumi võrdlemise testid ja MS Excel'i moodul nende läbiviimiseks". Tööga, mis annab teoreetilise ja põhjaliku ülevaate erinevatest mitteparameetrilistest kahe üldkogumi keskväärtuste võrdlemisel kasutatavatest testidest, saab tutvuda siin: http://www.eau.ee/~ktanel/baca_AIher_2005.pdf.

Töö osana valminud Exceli lisamooduli ja selle abifaili saab alla laadida aadressilt http://www.eau.ee/~ktanel/excel_addins/.

Lisamooduli rakendamiseks tekib peale selle installeerimist (analoogselt statistika-protseduuride paketi Data Analysis kasutuselevõtuga - vt pt 1.3) Exceli lisamoodulite saki (Add-Ins-sakk) alla valik |Kahe üldkogumi võrdlus|.

Lisamooduli tellimisaken on analoogne Exceli statistikaprotseduuride tellimisaknaga, määrata tuleb

• võrreldavate valimite andmed (võivad paikneda nii veergudes kui ka ridades),
• pealkirja olemasolu ette antud valimite esimeses reas/veerus,
• olulisuse nivoo (vaikimisi 0,05),
• võrreldavate valimite tüüp - sõltuvad või sõltumatud - ning soovitud test(id), NB!
  • korraga võib tellida mitu testi,
  • tellides sõltumatute valimite korral t-testi, teostatakse mõlemad, nii võrdseid kui ka erinevaid dispersioone eeldavad t-testid, ning lisaks ka F-test dispersioonide võrdlemiseks,
• väljundi asukoht,
• lisaselgituste soov (lisaks kõiksugu statistikute nimetustele/tähistustele ja arvutuste tulemustele kuvatakse väljundtabeleis ka vähe pikemad selgitused, sh lõppjäreldus).

Joonisel 42 on lisamoodulit "Kahe üldkogumi võrdlus" rakendatud tudengite testitulemuste võrdlemiseks märgitestiga.

Tulemused on identsed eelnevalt funktsiooni BINOM.TEST abil arvutatutega. Ainult lisaks täpsetele binoomjaotusel baseeruvatele p-väärtustele arvutab lisamoodul "Kahe üldkogumi võrdlus" ka ligikaudsed normaaljaotusel baseeruvad p-väärtused - taolise tegevuse mõte on selles, et mitmete mitteparameetriliste testide arvutuseeskirjad on nende rakendamiseks suurte valimite puhul liiga töömahukad, samas on kasutatavate teststatistikute jaotus suurte valimite puhul lähendav standardse normaaljaotusega ja sestap saab sellisel juhul ka p-väärtuste arvutamisel lähtuda standardsest normaaljaotusest (z-statistikust).
 

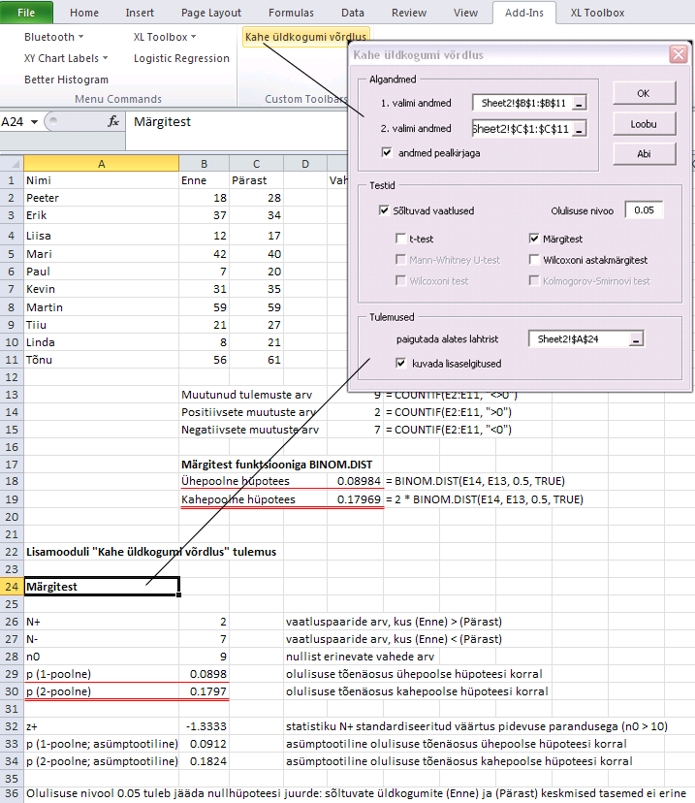
Joonis 42. Märgitesti rakendamine tudengite testitulemuste võrdlemiseks lisamooduliga "Kahe üldkogumi võrdlus".
 

Joonise 43 alaosadel on korraga teostatud t-test, Wilcoxoni test ja Komogorov-Smirnovi test võrdlemaks autot omavate ja mitte omavate esimese kursuse noormeeste nädalas tarbitavaid õllekoguseid. Joonisel 43A on ära toodud analüüside tellimisaken ning joonisel 43B osa lisaselgitustega varustatud väljundist - valimite kirjeldus ning t- ja F-testi tulemused. Joonisel 43C on ära toodud ülejäänud osa väljundist - Wilcoxoni ja Komogorov-Smirnovi testi tulemused.

Tulemustest nähtub, et autot omavad noormehed joovad nädalas keskmiselt 1,1 liitrit enam õlut kui autot mitte omavad noormehed (keskmised nädalas tarbitavad õllekogused on vastavalt 2,5 ja 1,4 liitrit), samas ei saa seda erinevust lugeda statistiliselt oluliseks (erinevatele dispersioonidele vastav t-test, p = 0,19). Küll võib varieeruvuse võrreldavates gruppides lugeda statistiliselt oluliselt erinevaks (F-test, p < 0,001) - seetõttu tuleb keskmiste võrdlemisel vaadata erinevatele dispersioonidele vastava t-testi tulemusi.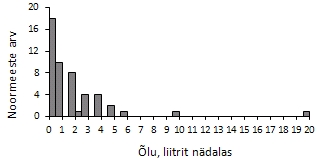

Iseküsimus on muidugi F- ja t-testi eelduste täidetus - noormeeste nädalas tarbitud õllekogused ei jaotu kohe kindlasti normaaljaotuse järgi (vt kõrvalolev joonis). Seetõttu on korrektsem kasutada autot omavate ja mitte omavate esimese kursuse noormeeste nädalas tarbitavate õllekoguste võrdlemiseks mitteparameetrilisi teste. Joonisel 43C ongi esitatud neist kahe tulemused.

Wilcoxoni testi täpse p-väärtuse arvutamiseks on andmeid liiga palju, mistõttu tuleb järeldused teha asümptootilise p-väärtuse alusel. Sarnaselt t-testile ei anna ka Wilcoxoni ja Komogorov-Smirnovi test alust lugeda autot omavate ja mitte omavate esimese kursuse noormeeste nädalas tarbitavaid õllekoguseid statistiliselt oluliselt erinevateks (vastavalt p = 0,42 ja p = 0,88). See, et p-väärtused suuremad, kui t-testi puhul, on loomulik, sest mõlemad mitteparameetrilised testid kontrollivad üldisemaid hüpoteese - Wilcoxoni test kahe valimi elementide mittejuhuslikku segunemist ja Kolmogorov-Smirnovi test jaotuste erinevust.
 

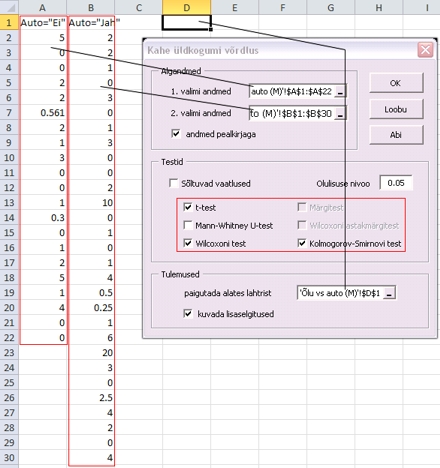
Joonis 43A. Autot omavate ja mitte omavate esimese kursuse noormeeste nädalas tarbitavate õllekoguste võrdlus lisamooduliga "Kahe üldkogumi võrdlus" - analüüside tellimine.
 

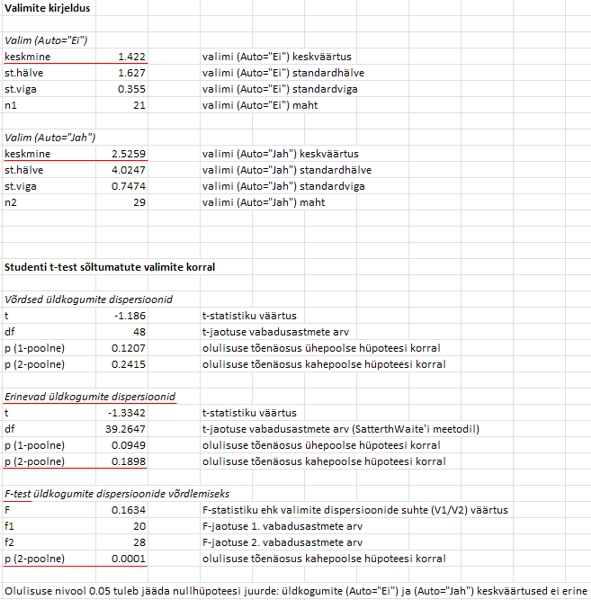
Joonis 43B. Autot omavate ja mitte omavate esimese kursuse noormeeste nädalas tarbitavate õllekoguste võrdlus lisamooduliga "Kahe üldkogumi võrdlus" - valimite kirjeldus ning t-test.
 

Joonis 43C. Autot omavate ja mitte omavate esimese kursuse noormeeste nädalas tarbitavate õllekoguste võrdlus lisamooduliga "Kahe üldkogumi võrdlus" - Wilcoxoni ja Komogorov-Smirnovi test.