|
Hüpoteeside
kontrollimise usalduspiiridega
Juhul,
kui kontrollitavaks hüpoteesiks on mingi andmete
alusel hinnatud suuruse erinevus konstandist, tehakse
otsus sageli 95%-lise usaldusintervalli alusel:
- kui
konstant, millega andmeist arvutatud suurust võrreldakse,
jääb usalduspiiride vahele, siis ei ole
alust väita, et arvutatud suurus erineb antud
konstandist;
- kui
aga onstant jääb usaldusintervallist väljapoole,
on arvutatud suurus konstandist statistiliselt oluliselt
erinev (p < 0,05).
Näiteks
soovides testida, kas esimese kursuse neidude keskmine
pikkus erineb Eesti naiste keskmisest pikkusest 168
cm, piisab, kui võrrelda konstanti 168 neidude
keskmise pikkuse 95%-lise usaldusintervalliga.
Kui
oletada, et on täpselt teada, kui varieeruvad
on esimese kursuse neidude pikkused - pikkuse standardhälve
on 6,5 cm -, on keskmise pikkuse 95%-line usaldusintervall
leitav funktsiooniga CONFIDENCE.NORM.
Kui
pikkuse dispersiooni täpselt teada pole - ja
enamasti see on nii -, tuleb dispersioon olemasolevatest
andmetest hinnata ja keskmise pikkuse 95%-line usaldusintervall
on leitav funktsiooniga CONFIDENCE.T (Joonis 32).
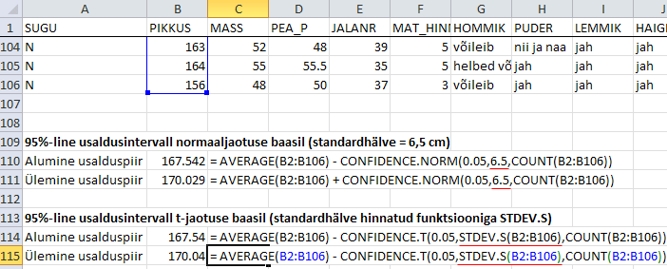
Joonis
32. Neidude keskmise pikkuse usaldusintervalli hindamine
funktsioonidega CONFIDENCE.NORM ja CONFIDENCE.T.
Et
Eesti naiste keskmine pikkus 168 cm jääb
esimese kursuse neidude keskmise pikkuse 95% usaldusintervalli
sisse: 167,5<168<170,0, siis ei ole alust lugeda
tõestatuks alternatiivset hüpoteesi keskmise
pikkuse erinevusest 168 sentimeetrist ja tuleb jääda
nullhüpoteesi juurde: esimese kursuse neidude
keskmine pikkus ei erine 168 sentimeetrist.
Hea
asi hüpoteeside kontrollimisel usalduspiiridega
on see, et kui nüüd soovida testida, kas
esimese kursuse neidude keskmine pikkus erineb maailma
naiste keskmisest pikkusest 154 cm, ei pea midagi
uuesti arvutama, piisab, kui võrrelda arvu
154 juba leitud usaldusintervalliga - kuna 154 ei
jää usalduspiiride vahele, võib lugeda
tõestatuks, et esimese kursuse neidude keskmine
pikkus erineb maailma naiste keskmisest pikkusest
154 cm (seejuures p < 0,05).
|