|
Regressioonanalüüs
funktsioonide abil
Funktsioonide
abil on Excelis võimalik teostada nii lihtsat
kui ka mitmest lineaarset regressioonanalüüsi
ning sobitada andmetele ka eksponentfunktsiooni. Kõigil
juhtudel on võimalik nii funktsiooni parameetrite
ja prognoosi headuse hindamine kui ka funktsioontunnuse
väärtuste prognoosimine ette antud argumenttunnuste
väärtuste korral.
Lihtne
lineaarne regressioonanalüüs
Lihtsa
lineaarse regressioonivõrrandi
y
= a + bx,
kus
y on uuritav ehk funktsioontunnus ja x
on argumenttunnus, parameetrite a ja b
hindamiseks Excelis on lihtsaim viis kasutada vastavalt
funktsioone INTERCEPT ja SLOPE. Prognoosi headust
kirjeldav determinatsioonikordaja R2
on hinnatav funktsiooniga RSQ ja mudeli standardviga
funktsiooniga STEYX.
Kõigi
nende funktsioonide puhul tuleb ühte moodi ette
anda
- funktsioontunnuse
y andmete blokk (Known_y's) ja
- argumenttunnuse
x andmete blokk (Known_x's).
Joonisel
55 on näidatud lihtsa lineaarse regressioonanalüüsi
teostamist funktsioonide INTERCEPT, SLOPE, RSQ ja
STEYX abil prognoosimaks noormeeste kehamassi nende
pikkuse alusel.
Tulemused
on identsed protseduuriga Regression arvutatutele:
- noormeeste
kehamass on nende pikkuse abil prognoostav valemist
Kehamass
= -97,0 + 0,978*Pikkus,
- kusjuures
antud mudel kirjeldab ära 21,0% noormeeste
kehamasside tegelikust varieeruvusest (R2
= 0,21) ja keskmiselt osutub prognoositud kehamass
valeks 13,1 kg võrra (SEM = 13,1).
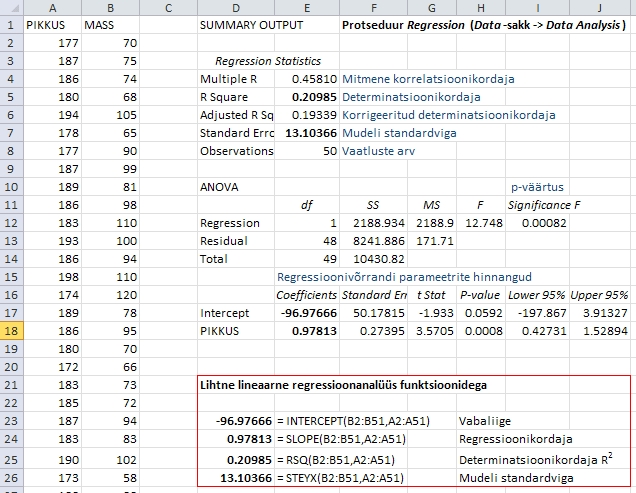
Joonis
55. Lihtne lineaarne regressioonanalüüs
funktsioonidega INTERCEPT, SLOPE, RSQ ja STEYX prognoosimaks
noormeeste kehamassi nende pikkuse alusel; võrdluseks
on ära toodud ka protseduuriga Regression
teostatud sama analüüsi tulemused, kusjuures
nii funktsioonidega kui ka protseduuriga Regression
arvutatavad väärtused on esitatud paksus
kirjas.
Mitmene
lineaarne regressioonanalüüs
Mahukaima
väljundi annab tulemuseks funktsioon LINEST,
mis võimaldab teostada nii lihtsat kui ka mitmest
lineaarset regressioonanalüüsi ning sobitada
andmetele ka argumenttunnuse funktsioone sisaldavaid
mudeleid (näiteks kõrgema astme polünoome).
Funktsioon LINEST on massiivifunktsioon (väljundiks
on väärtuste tabel, mitte üksikväärtus),
mille tulemuseks on sõltuvalt funktsiooni argumentidest
kas vaid regressioonikordajad või regressioonikordajad
pluss hulk teisi regressioonanalüüsiga kaasnevaid
karakteristikuid.
Funktsioon
LINEST rakendamiseks tuleb (Joonis 56)
-
selekteerida Exceli töölehel väljundtabeli
jagu lahterid (kui palju täpselt, sõltub
funktsiooni LINEST kahest viimasest argumendist);
-
anda ette funktsiooni argumendid:
- funktsioontunnuse
y andmete blokk (Known_y's),
- argumenttunnus(t)e
x andmete blokk (Known_x's),
- argument
Const väärtustega TRUE (vaikimisi
väärtus, hinnatav mudel sisaldab vabaliiget)
või FALSE (hinnatav mudel ei sisalda vabaliiget),
- argument
Stats väärtustega FALSE
-
vaikimisi väärtus, arvutatakse ja
väljastatakse vaid mudeli parameetrite
- so vabaliikme (argumendi Const = TRUE
korral) ja regressioonikordja(te) - hinnagud,
või
TRUE
- lisaks
mudeli parameetrite hinnangutele väljastatakse
ka
-
parameetrite hinnangute standardvead,
-
regressiooniseose headust kirjeldavad determinatsioonikordaja
R2 ja mudeli standardvea SEM
väärtused,
-
F-statistiku (e F-suhte) väärtus,
F-suhte nimetaja vabadusastmete arv (Df2)
ning nii mudelile kui ka mudeli jäägile
vastavad ruutude summade väärtused
(SSmudel ja SSjääk)
mudeli dispersioonanalüüsi tabelis;
-
vajutada Ctrl+Shift ja Enter (või
OK).
NB!
Mitmese regressioonanalüüsi korral peavad
argumenttunnused paiknema üksteise kõrval,
et neid saaks ette anda ühe pideva andmeblokina.
Samuti eeldab funktsioon LINEST, et ette antud funktsioon-
ja argumenttunnuste väärtuste blokid ei
sisalda puuduvaid väärtuseid, vastasel korral
lõpeb funktsiooni rakendamine veateatega.
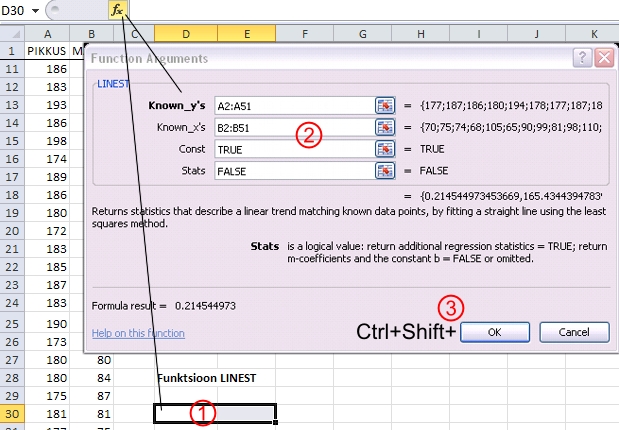
Joonis
56. Funktsiooni LINEST rakendamine prognoosimaks noormeeste
kehamassi nende pikkuse alusel lineaarse regressioonanalüüsi
abil.
Väljundtabeli,
mille jagu lahtreid tuleb enne funktsiooni LINEST
rakendamist blokki võtta,
- ridade
arv on üks argumendi Stats = FALSE
ja viis argumendi Stats = TRUE korral,
- veergude
arv on võrdne mudeli parameetrite arvuga,
st vabaliige pluss argumentide arv.
St,
et näiteks mitmese regressioonivõrrandi
y
= a + b1*x1 + b2*x2
+ … + bm*xm
korral
on funktsiooni LINEST laiendatud väljundtabelis
viis rida ja m+1 veergu (m on argumenttunnuste
arv):
|
bm
|
bm-1
|
...
|
b1
|
a
|
|
se(bm)
|
se(bm-1)
|
...
|
se(b1)
|
se(a)
|
|
R2
|
SEM
|
|
|
|
|
F
|
Df2
|
|
|
|
|
SSmudel
|
SSjääk
|
|
|
|
NB!
Regressioonivõrrandi parameetrid paiknevad
funktsiooni LINEST väljundis nö tagurpidi
- vasakult poolt esimesel kohal on viimane regressioonikordaja
ning kõige viimasel kohal mudeli vabaliige
(või selle puudumisel esimene regressioonikordaja).
Joonisel
57 on esitatud funktsiooni LINEST süntaks ja
tulemused prognoosimaks noormeeste kehamassi nende
pikkuse alusel lineaarse regressioonanalüüsi
abil. Esitatud on nii funktsiooni LINEST vaikimisi
väljund, mis sisaldab üksnes regressioonivõrrandi
parameetreid, kui ka laiendatud väljund. Võrdluseks
on esitatud ka sama ülesande lahendamisel protseduuriga
Regression saadud tabelid ning vaid üksikväärtusi
väljastavate funktsioonide INTERCEPT, SLOPE,
RSQ ja STEYX tulemused.
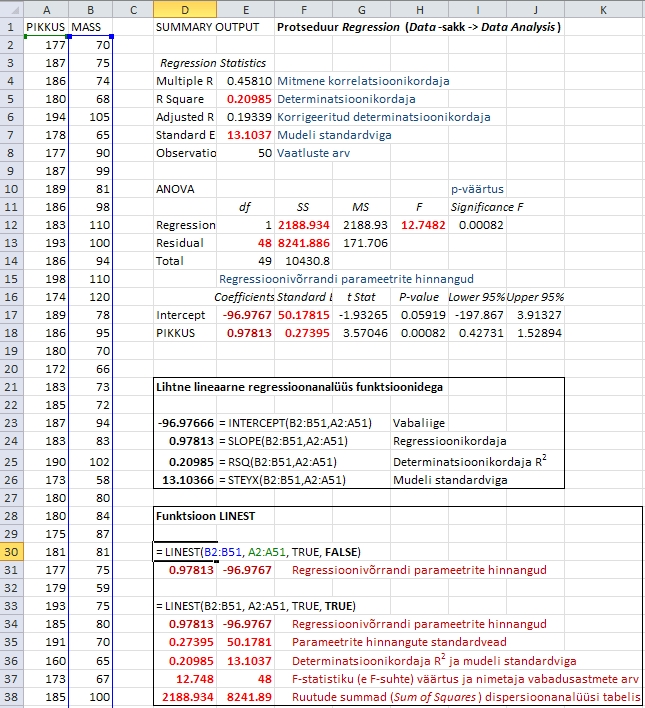
Joonisel
57. Funktsiooni LINEST süntaks ning vaikimisi
produtseeritav ja laiendatud väljund prognoosimaks
noormeeste kehamassi nende pikkuse alusel lineaarse
regressioonanalüüsi abil; võrdluseks
on esitatud sama ülesande lahendamisel protseduuriga
Regression saadud tabelid, milles ka funktsiooni LINEST
poolt väljastatavad suurused on punases paksus
kirjas, ning vaid üksikväärtusi väljastavate
funktsioonide INTERCEPT, SLOPE, RSQ ja STEYX tulemused.
Nii
nagu varemalt kirjeldatud protseduuri Regression
(pt. 7.1) ning
antud punkti alguses kirjeldatud funktsioonide INTERCEPT,
SLOPE, RSQ ja STEYX tulemuste alusel, saab nüüdki
järeldada, et
- noormeeste
kehamass on nende pikkuse abil prognoostav valemist
Kehamass
= -97,0 + 0,978*Pikkus,
- kusjuures
mudel kirjeldab ära 21,0% noormeeste kehamasside
tegelikust varieeruvusest (R2
= 0,21) ja keskmiselt osutub prognoositud kehamass
valeks 13,1 kg võrra (SEM = 13,1).
Aga
lisaks saab funktsiooni LINEST laiendatud väljundis
toodud suuruste alusel testida ka hüpoteese nii
mudeli kui terviku statistilise olulisuse kui ka üksikute
liikmete statistilise olulisuse kohta.
Mudeli
statistilise olulisuse testimine baseerub F-statistikul
(ehk F-suhtel), mis on nullhüpoteesi kehtides
F-jaotusega parameetritega Df1 ja
Df2. F-suhte väärtus ja
selle nimetajale vastav vabadusastmete arv Df2
sisalduvad ka funktsiooni LINEST laiendatud väljundis
(Joonis 58). F-suhte lugeja vabadusastmete arv Df1
on juhul, kui mudel sisaldab vabaliiget, leitav valemist
Df1 = n - Df2
- 1, vabaliikme puudumisel (funktsiooni LINEST argument
Const = FALSE) aga valemist Df1
= n - Df2, suurus n
tähistab valimi mahtu. Nn mudeli p-väärtus
on arvutatav funktsiooniga F.DIST.RT, mille esimeseks
argumendiks on F-statistiku väärtus ning
teiseks ja kolmandaks argumendiks vastavalt F-jaotuse
parameetrid Df1 ja Df2.
Iga
üksiku regressioonivõrrandi parameetri
statistilise olulisuse testimine baseerub t-statistikul,
mis on arvutatav kui parameetri hinnangu suhe oma
standardveasse (ja need suurused sisalduvad funktsiooni
LINEST väljundis). Parameetri statistilist olulisust
näitav p-väärtus on arvutatav funktsiooniga
T.DIST.2T, mille esimeseks argumendiks on t-statistiku
absoluutväärtus ning teiseks argumendiks
ka terve mudeli statistilise olulisuse testimisel
kasutatud funktsiooni LINEST väljundis sisalduv
suurus Df2.
Nagu
näha jooniselt 58, on funktsiooni LINEST väljundi
baasil arvutatud p-väärtused identsed protseduuri
Regression poolt väljastatutega.
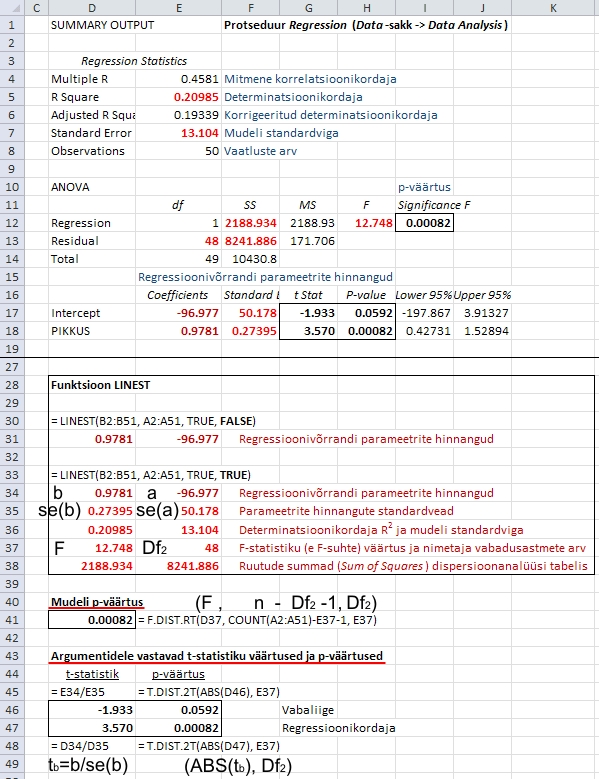
Joonis
58. Hüpoteeside testimine funktsiooni LINEST
tulemuste alusel; võrdluseks on esitatud sama
ülesande lahendamisel protseduuriga Regression
saadud tabelid.
Eksponentfunktsioon
Hindamaks
uuritava tunnuse y ja argumenttunnuste x1,
…, xm vahelist seost kujul
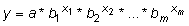
ehk
logaritmilisel skaalal kujul
ln(y)
= ln(a) + x1*ln(b1)
+ … + xm*ln(bm)
on
kasutatav funktsioon LOGEST.
Funktsiooni
LOGEST argumendid ja ka väljund on identsed funktsiooniga
LINEST.
Joonisel
59 on kujutatud noormeeste kehamassi prognoosimist
nende pikkuse alusel eksponentfunktsiooniga kujul
Pikkus
= a*bKehamass.
Tulemustest
järeldub, et regressioonivõrrand on kujul
Pikkus
= 8,21*1,013Kehamass,
kusjuures
mudel kirjeldab ära 24,0% noormeeste kehamasside
tegelikust varieeruvusest (R2 =
0,24).
NB!
Ülejäänud parameetrite - ja eelkõige
standardvigade - tõlgendamisel peab aga silmas
pidama asjaolu, et kõik funktsiooni LOGEST
laiendatud väljundis sisalduvad tulemused (arvutatakse,
kui argument Stats = TRUE) on leitud logaritmilisel
skaalal, antud juhul siis mudeli
ln(Pikkus)
= ln(8,21) + Kehamass*ln(1,013)
baasil.
St, et funktsioon LOGEST väljastab parameetrite
a ja b hinnangute juurde standardvead
kujul se[ln(b)] ja se[ln(a)].
Mudeli statistilise olulisuse testimine funktsiooni
LOGEST poolt väljastatud F-statistiku väärtuse
ja selle nimetaja vabadusastmete arvu Df2
alusel käib küll analoogselt funktsiooni
LINEST puhul näidatule (vt Joonis 59) - tulemuseks
on p < 0,001, st mudel on statistiliselt
olulne -, aga hüpoteeside testimisel mudeli üksikute
argumentide tarvis tuleb t-statistiku arvutamisel
jagada parameetri logaritmitud väärtus funktsiooni
LOGEST poolt väljastatud standardveaga (vt Joonis
59).
NB!
Vaid ühe argumenttunnuse korral on eksponentfunktsiooni
kujul avalduv seos andmetele sobitatav ka graafiliselt
punktdiagrammi ja sellele lisatud trendijoonena. Ainult
et graafilisel lahendamisel on vastav funktsioon Excelis
defineeritud kujul
y
= A*eB*x
(e
= 2,718…) ehk logaritmilisel skaalal kujul
ln(y)
= ln(A) + B*x.
Kõrvutades
neid võrrandeid funktsiooni LOGEST poolt hinnatavatega
ilmneb, et mudeli vabaliige on nii funktsiooni LOGEST
kui ka eksponentsiaalse trendijoone puhul sama: a
= A (kus a ja A on vastavalt
funktsiooniga LOGEST ja eksponentsiaalse trendijoone
abil hinnatavad mudeli vabaliikmed).
Eksponentsiaalse trendijoone abil hinnatav regressioonikordaja
B on aga võrdne naturaallogaritmiga
funktsiooni LOGEST poolt hinnatud regressioonikordjast
b: B = ln(b).
See
seos funktsiooni LOGEST tulemuste ja eksponentsiaalse
trendijoone vahel ilmneb ka jooniselt 59, kus on täiendavalt
esitatud noormeeste kehamassi prognoosimine nende
pikkuse alusel eksponentsiaalse trendijoonega - regressioonivõrrand
joonisel on kujul
Pikkus
= 8,21*e0,012*Kehamass.
Võrrandi
vabaliige 8,209 on sama, mis funktsiooni LOGEST poolt
saadu, regressioonikordaja 0,012 on aga võrdne
naturaallogaritmiga funktsiooni LOGEST väljastatud
regressioonikordajast: 0,012 = ln(1,013).
Funktsiooni
LOGEST ja eksponentsiaalse trendijoone abil hinnatud
eksponentfunktsioonide samasust näitab ka see,
et determinatsioonikordaja R2 väärtus
on mõlemal juhul sama: R2
= 0,24.
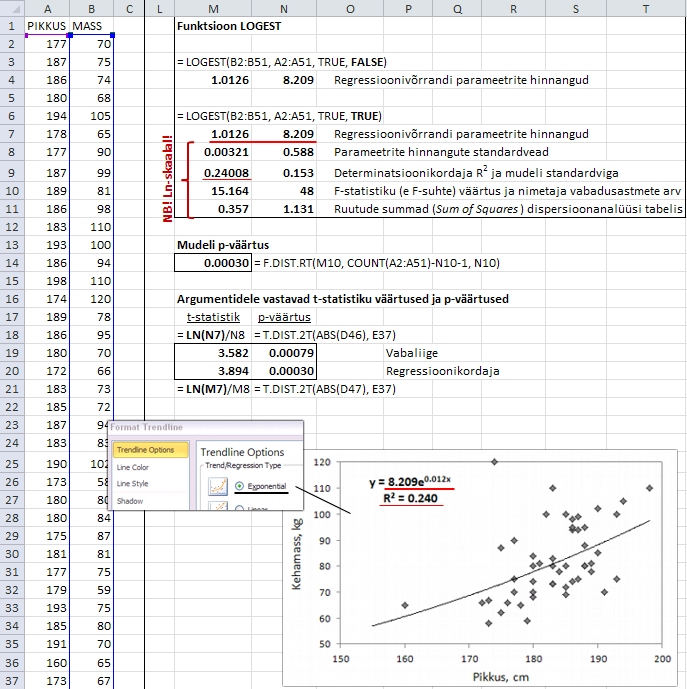
Joonis
59. Noormeeste kehamassi prognoosimine pikkuse alusel
eksponentfunktsiooni abil funktsiooniga LOGEST; võrdluseks
on esitatud ka sama ülesande lahendus graafiliselt
punktdiagrammi ja sellele lisatud eksponentsiaalse
trendijoone abil.
Prognoosimine
Prognoosimiseks
vastavalt lineaarsele regressioonivõrrandile
on Excelis kasutatavad funktsioonid FORECAST ja TREND
ning vastavalt eksponentvõrrandile funktsioon
GROWTH.
Funktsioon
FORECAST väljastab määratud lahtrisse
vaid ühele argumenttunnuse väärtusele
vastava prognoosi lineaarse regressioonivõrrandi
alusel ning talle tuleb ette anda
- väärtus,
millele vastavat prognoosi soovitakse leida (X),
- funktsioontunnuse
y andmete blokk (Known_y's) ja
- argumenttunnuse
x andmete blokk (Known_x's).
Funktsioonid
TREND ja GROWTH on mõlemad massiivifunktsioonid
ning nad võimaldavad arvutada prognoosid suurele
hulgale ette antud argumenttunnuse väärtustele
või mitmese regressiooni puhul argumenttunnuste
väärtuste komplektidele. Mõlema funktsiooni
rakendamiseks tuleb esmalt võtta blokki prognoositavate
väärtuste jagu lahtreid (ükskõik
kas veerus või reas), anda argumentidena ette
- funktsioontunnuse
y andmete blokk (Known_y's),
- argumenttunnus(t)e
x andmete blokk (Known_x's),
- väärtused,
millele vastavaid prognoose soovitakse leida (New_x's),
ja
- argumendi
Const väärtus TRUE (vaikimisi väärtus,
hinnatav mudel sisaldab vabaliiget) või FALSE
(hinnatav mudel ei sisalda vabaliiget)
ning
vajutada valemi rakendamiseks Ctrl+Shift ja
Enter (või OK).
NB!
Kui jätta funktsioonidele TREND ja GROWTH kolmas
argument New_x's ette andmata, arvutavad mõlemad
funktsioonid prognoosid kõigi andmeridade tarvis
vastavalt neis paiknevate argumenttunnus(t)e väärtustele.
Seejuures tuleks muidugi enne funktsioonide rakendamist
selekteerida andmestiku suuruse jagu tühje lahtreid
(näiteks andmestiku lõpus lisaveeruna),
kuhu prognoosid arvutada.
Joonisel
60 on näidatud, kuidas arvutada noormeeste hinnangulised
kehamassid etta antud pikkuste tarvis.
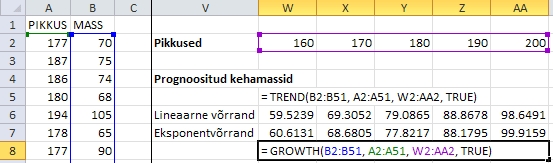
Joonis
60. Noormeeste kehamasside prognoosimine lineaarsest
ja eksponentvõrrandist funktsioonide TREND
ja GROWTH abil.
|