|
T-test
Kahe
üldkogumi keskväärtuste võrdlemine
sõltuvate valimite korral (paariviisiline võrdlus)
Sõltuvate
vaatlustega/mõõtmistega on tegu, kui
mõõdetud on samu või kõigi
katsetulemust potentsiaalselt mõjutada võivate
kriteeriumite poolest sarnaseid indiviide/objekte
enne ja pärast teatavat "katset" (enne
ja pärast ravimi manustamist, hommikul ja õhtul
jne). Taolisel juhul moodustuvad "enne ja pärast
sooritatud" mõõtmistest paarid
- igal indiviidil/objektil on üks mõõtmine
ühes ja teine mõõtmine teises grupis
("enne ja pärast"). Gruppide keskmiste
omavaheline võrdlemine on siis samaväärne
keskmise muutuse nulliga võrdlemisega.
Excelis
on kahe sõltuva (paaris) valimi keskmiste võrdlemiseks
kasutatav funktsioon T.TEST ja protseduur t-Test:
Paired Two Sample for Means.
Funktsiooni
T.TEST, mis annab tulemuseks vaid olulisuse tõenäosuse
p väärtuse, rakendamiseks tuleb panna
kursor lahtrisse, kuhu tulemust soovite, valida Exceli
funktsioonide hulgast või sisestada klaviatuurilt
funktsioon T.TEST ja anda ette (vt ka Joonis 36)
- mõlema
valimi andmete blokid (Array1 ja Array2),
- hüpoteesi
tüüp (Tails): 1 - ühepoolne
hüpotees (one-tailed distribution),
2 - kahepoolne hüpotees (one-tailed distribution),
- testi
tüüp lähtuvalt andmete struktuurist
ja varieeruvusest (Type): antud juhul 1 -
sõltuvad valimid (paired); ülejäänud
kaks tüüpi on: 2 - sõltumatud valimid
ja võrdsed dispersioonid (two-sample equal
variance (hoscedastic)) ning 3 - sõltumatud
valimid ja erinevad dispersioonid (two-sample
unequal variance).
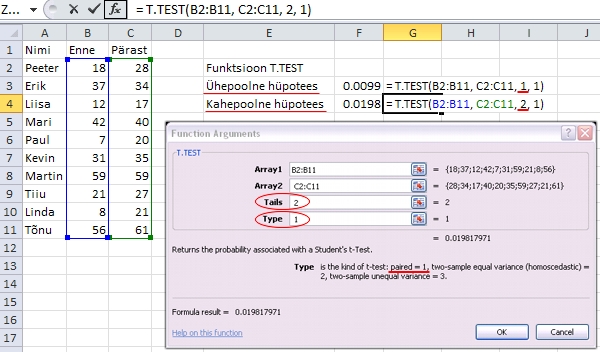
Joonis
36. Funktsiooni T.TEST rakendamine tudengite enne
ja pärast kursuse läbimist teostatud testi
tulemuste võrdlemiseks sõltuvate valimite
eeldusel.
Protseduur
t-Test: Paired Two Sample for Means (Data-sakk
-> Data Analysis) annab tulemuseks nii võrreldavaid
gruppe kirjeldavad karakteristikud kui ka t-testi
teostamisega kaasnevad arvutustulemused nii ühe-
kui ka kahepoolse hüpoteesi kontrollimiseks ning
selle rakendamiseks tuleb ette anda (vt Joonis 37)
- mõlema
valimi andmete blokid - Variable 1 Range
ja Variable 2 Range (seejuures võivad
andmed paikneda nii veerus kui ka reas),
- oletatav
keskväärtuste erinevus (vaikimisi null)
- Hypothesized Mean Difference,
- kui
andmete blokid sisaldavad esimeses reas/veerus nime,
tuleb teha "linnuke" märgendi Labels
ette,
- olulisuse
nivoo (vaikimisi 0,05) - Alpha,
- tulemuste
väljastamise asukoht (Output options):
samale töölehele (Output Range),
uuele töölehele (New Worksheet Ply)
või uude faili (New Workbook).
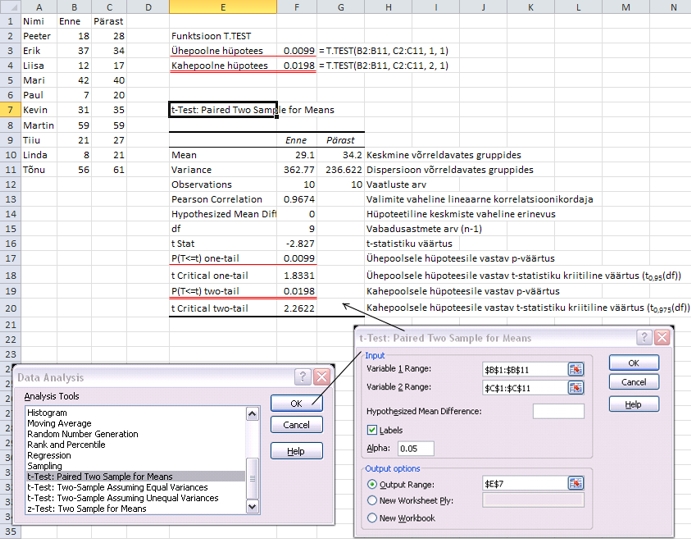
Joonis
37. Protseduuri t-Test: Paired Two Sample for Means
rakendamine tudengite enne ja pärast kursuse
läbimist teostatud testi tulemuste võrdlemiseks
sõltuvate valimite eeldusel.
Tulemustest
(Joonis 37) võib järeldada, et tudengite
testi tulemused enne ja pärast kursuse läbimist
on statistiliselt oluliselt erinevad (p = 0,020).
Ühepoolse hüpoteesina testivad nii funktsioon
T.TEST kui ka protseduur t-Test: Paired Two Sample
for Means alati seda, kas suurem valimi keskmine
on statistiliselt oluliselt suurem, kui väiksem
valimi keskmine. Kuna antud näite puhul on testi
tulemus pärast kursuse läbimist keskmiselt
kõrgem, näitabki ühepoolsele testile
vastav p-väärtus, et tudengite testi tulemused
pärast kursuse läbimist on statistiliselt
oluliselt paremad, kui enne kursuse läbimist
(p = 0,010).
Kahe
üldkogumi keskväärtuste võrdlemine
võrdsete dispersioonide korral
Kui
- võrreldavad
valimid on sõltumatud ja
- on
alust eeldada uuritava tunnuse võrdset varieeruvust
gruppides (NB! siin ei ole õige lähtuda dispersioonide erinevuse testist funktsiooniga
F.TEST, vaid sisulistest eelteadmistest ja kaalutlustest),
on
valimite keskmiste võrdlemiseks kasutatavad
funktsioon T.TEST ja protseduur t-Test: Paired
Two Sample Assuming Equal Variances abil.
Funktsioonile
T.TEST, mis annab tulemuseks vaid olulisuse tõenäosuse
p väärtuse, tuleb ette anda
- mõlema
valimi andmete blokid (Array1 ja Array2),
- hüpoteesi
tüüp (Tails): 1 - ühepoolne
hüpotees (one-tailed distribution),
2 - kahepoolne hüpotees (one-tailed distribution),
- testi
tüüp lähtuvalt andmete struktuurist
ja varieeruvusest (Type): antud juhul 2 -
sõltumatud valimid ja võrdsed dispersioonid
(two-sample equal variance (hoscedastic));
ülejäänud kaks tüüpi on:
1 - sõltuvad valimid (paired) ning
3 - sõltumatud valimid ja potentsiaalselt erinevad dispersioonid
(two-sample unequal variance).
Protseduuri
t-Test: Paired Two Sample Assuming Equal Variances
(Data-sakk -> Data Analysis) tellimisaknas
tuleb määrata:
- mõlema
valimi andmete blokid - Variable 1 Range
ja Variable 2 Range (seejuures võivad
andmed paikneda nii veerus kui ka reas),
- oletatav
keskväärtuste erinevus (vaikimisi null)
- Hypothesized Mean Difference,
- kui
andmete blokid sisaldavad esimeses reas/veerus nime,
tuleb teha "linnuke" märgendi Labels
ette,
- olulisuse
nivoo (vaikimisi 0,05) - Alpha,
- tulemuste
väljastamise asukoht (Output options):
samale töölehele (Output Range),
uuele töölehele (New Worksheet Ply)
või uude faili (New Workbook).
Joonisel
38 on esitatud sportivate ja mittesportivate neidude
keskmiste kehamasside võrdlemine nii funktsiooniga
T.TEST kui ka protseduurga t-Test: Paired Two Sample
Assuming Equal Variances (eeldame, et kehamasside varieeruvus on võrreldavates gruppides ühesugune). Tulemustest
nähtub, et kuigi kehamasside dispersioon sportimist
mitte harrastavate neidude hulgas on suurem
(protseduuri t-Test: Paired Two Sample Assuming
Equal Variances väljundtabelist nähtub,
et 131,7 kg2 sportivate neidude 86,1 kg2
vastu), ei ole see erinevus siiski statistiliselt
oluline (F-test, p = 0,16) ega anna alust kahelda algselt tehtud dispersioonide võrdsuse eelduses. Samuti ei ole statistiliselt
oluline keskmiste kehamasside vaheline erinevus (t-test,
p = 0,29); siiski võib ära märkida,
et sportivate neidude kehamass on pisut suurem.
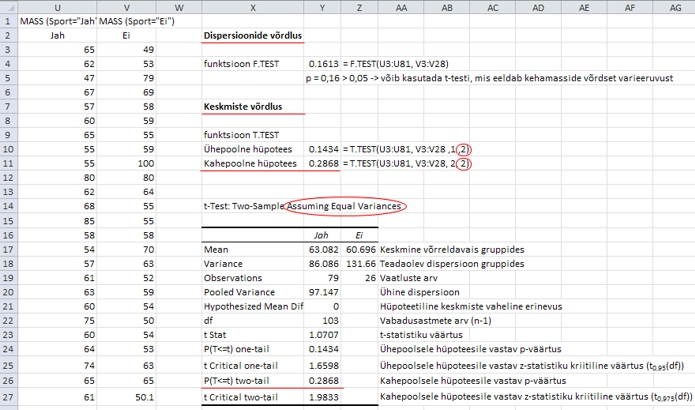
Joonis
38. Sportivate ja mittesportivate neidude keskmiste
kehamasside võrdlemine funkt-siooniga T.TEST
ja protseduuriga t-Test: Paired Two Sample Assuming
Equal Variances.
Kahe
üldkogumi keskväärtuste võrdlemine
erinevate dispersioonide korral
Kui
- võrreldavad
valimid on sõltumatud ja
- uuritava
tunnuse varieeruvus gruppides võib olla erinev (puudub eelinfo dispersioonide
võimalikust võrdusest; NB! siin ei ole korrektne lähtuda dispersioonide erinevuse testist funktsiooniga F.TEST),
on
valimite keskmiste võrdlemiseks kasutatavad
funktsioon T.TEST ja protseduur t-Test: Paired
Two Sample Assuming Unequal Variances.
Mõlemal
juhul on ette antavad argumendid ja väljund analoogsed
samas peatükis eelnevalt kirjeldatuga. Vaid protseduuri
t-Test: Paired Two Sample Assuming Unequal Variances
väljundtabelis on üks rida vähem -
et dispersioonid võivad olla erinevad, ei kasutata arvutamisel
enam kahe valimi ühist dispersiooni (Pooled
Variance).
|