|
F-test
Kahe
üldkogumi dispersioonide võrdlemiseks
on Excelis kasutatavad funktsioon F.TEST ja protseduur
F-Test: Two-Sample for Variances.
Seejuures
testib funktsioon F.TEST vaid kahepoolset hüpoteesi
kujul
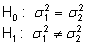
kus
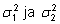 on vastavalt esimese ja teise valimi dispersioon,
ning protseduur F-Test: Two-Sample for Variances
vaid ühepoolset hüpoteesi kujul
on vastavalt esimese ja teise valimi dispersioon,
ning protseduur F-Test: Two-Sample for Variances
vaid ühepoolset hüpoteesi kujul
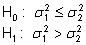
kus
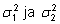 on vastavalt suurema ja väiksema varieeruvusega
valimi dispersioonid (st, et protseduur F-Test:
Two-Sample for Variances uurib alati, kas suurem
dispersioon on ka statistiliselt oluliselt suurem).
on vastavalt suurema ja väiksema varieeruvusega
valimi dispersioonid (st, et protseduur F-Test:
Two-Sample for Variances uurib alati, kas suurem
dispersioon on ka statistiliselt oluliselt suurem).
Funktsioonile
F.TEST, mis annab tulemuseks vaid olulisuse tõenäosuse
p väärtuse, tuleb ette anda mõlema
valimi andmete blokid (Array1 ja Array2).
Protseduur
F-Test: Two-Sample for Variances (Data-sakk
-> Data Analysis) annab tulemuseks nii võrreldavaid
gruppe kirjeldavad karakteristikud kui ka F-testi
teostamisega kaasnevad arvutustulemused ning selle
rakendamiseks tuleb ette anda:
- mõlema
valimi andmete blokid - Variable 1 Range
ja Variable 2 Range,
- kui
andmete blokid sisaldavad esimeses reas/veerus nime,
tuleb teha "linnuke" märgendi Labels
ette,
- olulisuse
nivoo (vaikimisi 0,05) - Alpha,
- tulemuste
väljastamise asukoht (Output options):
samale töölehele (Output Range),
uuele töölehele (New Worksheet Ply)
või uude faili (New Workbook).
Joonisel
39 on näha nii funktsiooni F.TEST kui ka protseduuri
F-Test: Two-Sample for Variances rakendamine
ja tulemused võrdlemaks sportivate ja mittesportivate
neidude kehamasside varieeruvust. Tulemustest nähtub,
et kuigi kehamasside dispersioon sportimist mitte
harrastavate neidude hulgas on märksa suurem
(protseduuri F-Test: Two-Sample for Variances
väljundtabelist nähtub, et 131,7 kg2
sportivate neidude 86,1 kg2 vastu), ei
ole see erinevus siiski statistiliselt oluline (kahepoolsele
hüpoteesile vastav p-väärtus funktsiooni
F.TEST tulemusena on 0,16). Tõestatuks ei saa
lugada ka ühepoolset hüpoteesi (protseduuri
F-Test: Two-Sample for Variances poolt väljastatud
ühepoolsele hüpoteesile vastav p-väärtus
on 0,081).
NB!
Et kahepoolsele hüpoteesile vastav olulisuse
tõenäosus võrdub kahekordse ühepoolsele
hüpoteesile vastava olulisuse tõenäosusega,
saab mõlemat tüüpi hüpoteese
kontrollida nii funktsiooniga F.TEST kui ka protseduuriga
F-Test: Two-Sample for Variances, peab üksnes
meeles pidama, mis tüüpi hüpoteesi
kumbki neist kontrollib ja siis vajadusel tulemuse
kahega jagama või korrutama.
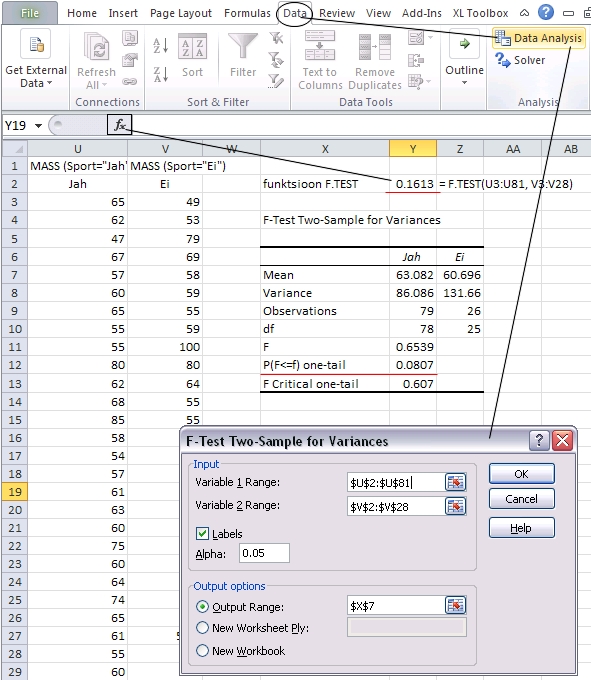
Joonis
39. Sportivate ja mittesportivate neidude kehamasside
varieeruvuse võrdlemine funkt-siooniga F.TEST
ja protseduuriga F-Test: Two-Sample for Variances.
|