|
Spearmani
e astakkorrelatsioonikordaja
Kui
uuritavate arvtunnuste näol on tegu pidevate
ja sümmeetrilise jaotusega tunnustega, on loomulikeim
seosekordaja Pearsoni e lineaarne korrelatsioonikordaja,
mis mõõdab kahe arvtunnuse vahelise
lineaarse seose tugevust ja suunda. Kui aga tunnused
ei ole normaaljaotusega, leidub üksikuid erandlikke
väärtuseid või ilmneb hajuvusdiagrammilt
küll kasvav või kahanev, aga mittelineaarne
seos, on mõttekas kasutada seose kirjeldamiseks
lineaarse korrelatsioonikordaja asemel (või
kõrval) Spearmani e astakkorrelatsioonikordajat.
Astakkorrelatsioonikordaja,
mis mõõdab kahe arvtunnuse vahelise
monotoonse seose tugevust ja suunda, arvutamiseks
Excelis valmis vahendid puuduvad. Aga teades, et astakkorrelatsioonikordaja
näol on tegu tavalise lineaarse korrelatsioonikordajaga
väärtuste astakute ehk järjekorranumbrite
vahel, saab seda kordajat arvutada ikkagi ka Excelis.
Astakkorrelatsioonikordaja
arvutamiseks tuleb
-
arvutada uuritavate tunnuste kõrvale nende
astakud funktsiooniga RANK.AVG (Joonis 48),
-
rakendada funktsiooni CORREL (või PEARSON)
leitud astakutele (Joonis 49).
NB!
Astakute arvutamiseks ei tohi kasutada funktsiooni
RANK.EQ (või vanema Exceli funktsiooni RANK),
sest erinevalt funktsioonist RANK.AVG, mis võrdsete
väärtuste korral võtab nende astakuks
järjekorranumbrite keskmise (näiteks kui
4. ja 5. väärtus on võrdsed, saab
nende mõlema astakuks 4,5), võtab funktsioon
RANK.EQ võrdsete väärtuste astakuks
vähima järjekorranumbri (kui 4. ja 5. väärtus
on võrdsed, saab nende mõlema astakuks
4). Astakkorrelatsiooni arvutusvalem eeldab, et võrdsete
väärtuste astakuks on just nimelt nende
järjekorranumbrite keskmine - so funktsiooniga
RANK.AVG leitud suurus.
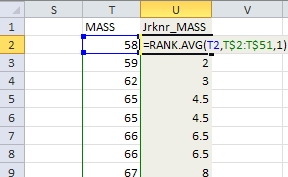
Joonis
48. Noormeeste kehamassi astakute arvutamine funktsiooniga
RANK.AVG.
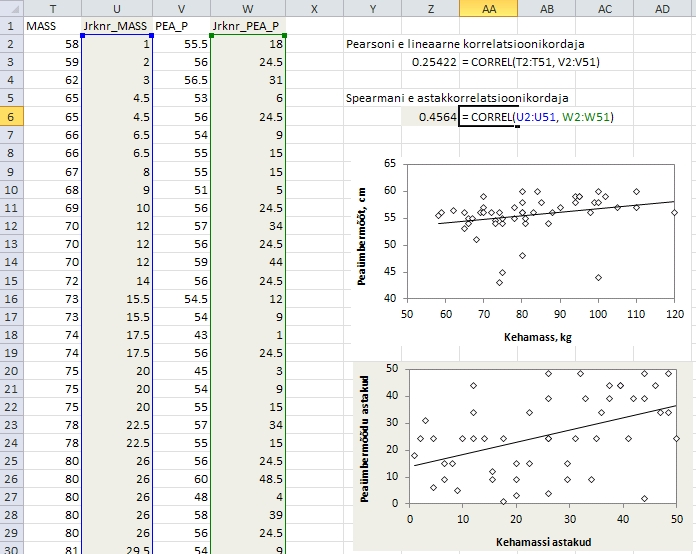
Joonis
49. Noormeeste kehamassi ja peaümbermõõdu
vahelise astakkorrelatsioonikordaja arvutamine (võrdluseks
on ära toodud ka lineaarne korrelatsioonikordaja).
Nagu
jooniselt 49 näha, on noormeeste kehamassi ja
peaümbermõõdu vahel nõrk
positiivne lineaarne seos (lineaarne korrelatsioonikordaja
r = 0,254) aga keskmise tugevusega positiivne
monotoonne seos (astakkorrelatsioonikordaja ρ
= 0,456). Seose tugevuse sedavõrd suure erinevuse
põhjuseks on eelkõige mõned erandlikud
väärtused (vt ülemist hajuvusdiagrammi
joonisel 49), mis mõjutavad märgatavalt
tunnuste vahelist lineaarset seost. Astakute vahelist
seost kujutaval hajuvusdiagrammil (alumine diagramm
joonisel 49) paiknevad punktid hajusamalt, aga puuduvad
teistest hälbivad erandlikud väärtused
- kokkuvõttes tähendab see tugevamat seost.
|