Kavalad funktsioonid ja valemid

Tundes hästi MS Exceli funktsioone, on teinekord võimalik lahendada esmapilgul keeruka ja töömahukana näivaid ülesandeid vaid ühe arvutuskäsuga. Järgnevalt ongi esitatud mõningad kas Excelis juba olemasolevad või siis Exceli funktsioonide loogikat kasutavad valemid erinevate arvutuste teostamiseks.

NB! Kõik järgnevalt esitatud valemid on korrektsed inglise keele seadistustes Exceli puhul, eesti keele seadistustes Exceli puhul peab arvudes olema punkti asemel koma ja funktsioonide argumentide eraldajaks koma asemel semikoolon.
 

Tinglik keskmine, summa ja loendus

Exceli funktsioonid AVERAGEIF ja AVERAGEIFS, SUMIF ja SUMIFS ning COUNTIF ja COUNTIFS võimaldavad arvutada vastavalt keskmist, summat ning vaatluste arvu vaid teatud tingimustele vastavatest andmebaasi veergudest (või ridadest). Seejuures võib tingimus käia nii samades vaatlusalustes lahtrites paiknevate väärtuste kui ka teistes veergudes (või ridades) paiknevate väärtuste kohta. IF-lõpuga funktsioonid võimaldavad ette anda vaid ühe tingimuse, IFS-lõpuga funktsioonid aga kuni 127 tingimust.

Funktsioonide AVERAGEIF ja SUMIF süntaks on identne:

• esimese argumendina tuleb määrata lahtriblokk, mille kohta käib kontrollitav tingimus (võib olla sama, kui keskmise või summa arvutuste aluseks olev lahtriblokk; Range),
• teiseks argumendiks on kontrollitav tingimus (Criteria) - kas konkreetne väärtus, viide väärtust sisaldavale lahtrile või võrdlus mingi väärtusega (võrdlus väärtusega mingis lahtris ei ole võimalik, st, et kui näiteks lahtris A2 on väärtus 4, siis on mõeldavad tingimused kujul "=4", "=A2", ">4", aga mitte kujul ">A2"),
• kolmandaks argumendiks on arvutuste aluseks olev lahtriblokk (Average_range või Sum_range).

Funktsiooni COUNTIF puhul kolmandat argumenti, millega anda ette kokkuloetavaid väärtuseid sisaldav lahtriblokk, pole - kokku loetakse tingimusele vastavad väärtused samast, esimese argumendiga (Range) ette antud lahtriblokist.

Funktsioonide AVERAGEIFS ja SUMIFS puhul on

• arvutuste aluseks olev lahtriblokk esimene argument (Average_range või Sum_range),
• millele järgnevad paarikaupa tingimuse aluseks olev lahtriblokk ja tingimus Criteria_range1, Criteria1, Criteria_range2, Criteria2, …).

Funktsiooni COUNTIFS puhul esimene arvutuste aluseks olev lahtriblokk puudub - kokku loetakse tingimus(t)ele vastavad väärtused esimese argumendiga (Criteria_range1) ette antud lahtriblokist.

NB! Erinevalt funktsioonist COUNT, mis loeb kokku vaid arvulised väärtused, toimivad funktsioonid COUNTIF ja COUNTIFS sama moodi nii arvuliste kui ka mittearvuliste väärtuste korral olles seega pigem funktsiooni COUNTA edasiarenduseks.

Jooonisel 71 on rakendatud tinglike arvkarakteristikute valemeid tudengite andmestiku näitel.
 

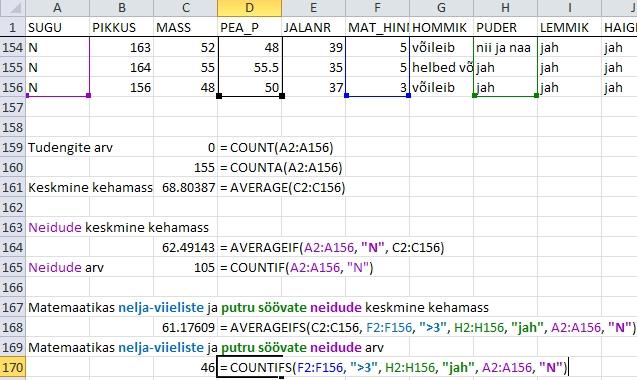
Joonis 71. Tinglike arvkarakteristikute leidmine Excelis; tingimuse aluseks olevad lahtrid ja nendele järgnevad tingimused on esitatud sama värviga, arvutuste aluseks olevad lahtrid, kui need on eraldi argumendiks, on mustas kirjas.
 

Tinglikud arvkarakteristikud funktsioonide IF ja OR abil

Eelmises punktis käsitletud tinglike arvkarakteristikute funktsioonidel on mitmeid puuduseid:

• esiteks on olemas funktsioonid vaid keskmise, summa ja vaatluste arvu tarvis, aga mitte teiste, samuti sageli kasutatavate arvkarakteristikute jaoks,
• teiseks ei ole võimalik määrata tingimusi kujul "üks või teine" - a'la leida keskmist pikkust tudengitel, kes kaaluvad alla 60 kg või üle 80 kg;
• kolmandaks ei saa tingimuste koostamisel kasutada teisi Exceli funktsioone.

Lahenduseks on funktsioonide IF ja OR kasutamine massiivifunktsioonidena (st, et nende rakendamiseks tuleb vajutada Ctrl+Shift ja Enter) statistikafunktsioonide siseselt - esmalt valitakse välja vaid ette antud tingimustele vastavad andmebaasi read (või veerud) ja seejärel rakendatakse soovitud statistikafunktsiooni neile välja valitud ridades (või veergudes) paiknevatele väärtustele.

Näiteks tudengite andmebaasis on tudengite sugu määratud lahtrites A2:A156 paiknevate väärtustega M ja N ning tudengite kehamass on lahtrites C2:C156. Tütarlaste keskmine pikkus on siis leitav nii funktsioonidega

= AVERAGEIF(A2:A156, "N", C2:C156)

ja

= AVERAGEIFS(C2:C156, A2:A156, "N")

kui ka funktsiooniga

= AVERAGE( IF(A2:A156="N", C2:C156, "") ).

NB! Et viimase funktsiooni näol on tegu massiivifunktsiooniga, tuleb selle rakendamiseks vajutada Ctrl+Shift ja Enter.

Viimast valemit modifitseerides on võimalik arvutada ka teisi tinglikke karakteristikuid ja testida hüpoteesegi (vt ka Joonis 72). Näiteks valem kujul

= MEDIAN( IF(A2:A156="N", C2:C156, "") ).

annab tulemuseks neidude kehamassi mediaani, valem kujul

= CORREL( IF(A2:A156="N", C2:C156, ""), IF(A2:A156="N", B2:B156, "") )

annab tulemuseks neidude kehamassi ja pikkuse (veerus B) vahelise korrelatsioonikordaja, valem kujul

= T.TEST( IF(A2:A156="N", C2:C156, ""), IF(A2:A156="M", C2:C156, ""), 2, 2 )

viib aga läbi teist tüüpi t-testi võrdlemaks neidude ja noormeeste keskmisi kehamasse.

 
Lisaks võib tingimus sisaldada funktsioone. Näiteks soovides arvutada keskmist kehamassi tudengitel, kes kaaluvad keskmisest enam, saab kasutada valemit kujul

=AVERAGE( IF(C2:C156>AVERAGE(C2:C156), C2:C156, "") ),

keskmisest suurema pikkusega tudengite kehamassi mediaan on arvutatav aga valemist

=MEDIAN( IF(B2:B156>AVERAGE(B2:B156), C2:C156, "") ).

 
Soovides aga rakendada mitut tingimust samaaegselt, näiteks arvutada matemaatikas nelja-viieliste ja putru söövate neidude keskmist kehamassi, saab seda teha eelmises alapunktis käsitletud valemiga

= AVERAGEIFS(C2:C156, F2:F156, ">3", H2:H156, "jah", A2:A156, "N"),

aga viimane ei ole üldistav teistele funktsioonidele ega võimalda kasutada tingimustes valemeid.

Alternatiiv on kasutada valemit, milles kõik samaaegselt kehtima pidavad tingimused on määratud üksteise sees paiknevate IF-lausetega:

= AVERAGE( IF(F2:F156>3, IF(H2:H156="jah", IF(A2:A156="N", C2:C156, ""), ""), "") )

(tudengite matemaatika hinded paiknevad lahtrites F2:F156 ja info pudru söömise kohta lahtrites H2:H156).

Soovides arvutada keskmist pikkust tudengitel, kes kaaluvad alla 60 kg või üle 80 kg, st anda tingimust ette kujul "üks või teine", saab seda teha OR-funktsiooniga IF-funktsiooni siseselt:

= AVERAGE( IF( OR(C2:C156<60, C2:C156>80), B2:B156, "") ).

 
Ja viimaks, mitut IF-funktsiooni, OR-funktsioone nende siseselt ja lisaks ka valemitega ette antud tingimusi võib rakendada kõiki koos, saamaks suurest andmebaasist ilma mistahes sorteerimiste ja filtreerimisteta vaid ühe funktsiooniga kätte huvipakkuva arvkarakteristiku väärtust või hüpoteeside kontrolli tulemust. Näiteks alla 60 kg ja üle 80 kg kaaluvate matemaatikas keskmiselt parema hindega noormeeste pikkuse mediaan on leitav valemiga

= MEDIAN( IF( OR(C2:C156<60, C2:C156>80), IF(F2:F156>AVERAGE(F2:F156), IF(A2:A156="M", B2:B156, ""), ""), "") ).
 

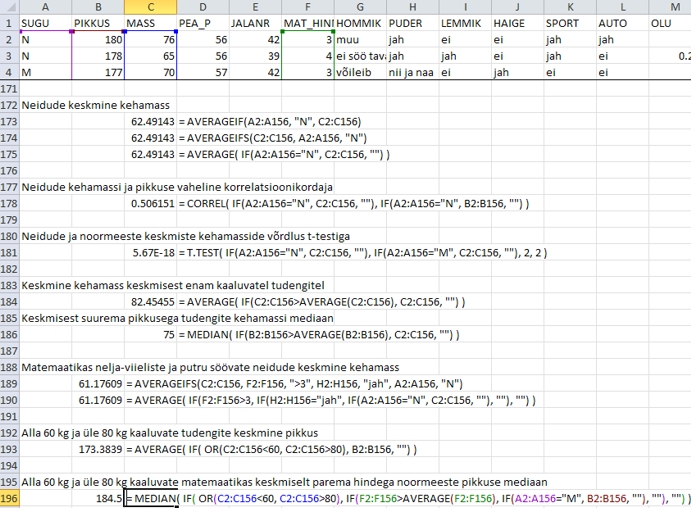
Joonis 72. Tinglike karakteristikute arvutamine Excelis funktsiooni IF abil.
 

Kaalutud keskmine

Mõnikord on vaja leida mingi näitaja keskmist väärtust kogu andmebaasis olukorras, kus seda andmebaasi ennast tegelikult kasutada pole, küll aga on olemas tabel keskmiste väärtustega mingites gruppides. Kui on teada ka gruppide suurused, on kogu andmebaasi keskmine arvutatav kaalutud keskmisena valemist

,

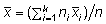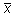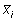kus ja on vastavalt kogu andmebaasi keskmine ja i. grupi keskmine, n ja n_i on vastavalt kogu andmebaasi suurus ja i. grupi suurus ning k on gruppide arv.

Excelis on kaalutud keskmist mugav arvutada funktsiooni SUMPRODUCT abil.

Joonisel 73 on näidatud esimese kursuse neidude keskmise kehamassi arvutamist kaalutud keskmisena, võttes aluseks tudengite arvud ja keskmised kehamassid mannapudru söömise ja mittesöömise alusel moodustatud gruppides.
 

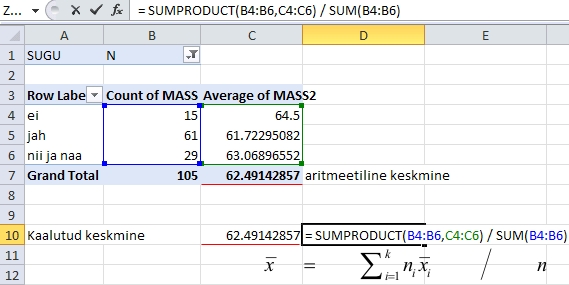
Joonis 73. Kaalutud keskmise arvutamine MS Excelis.
 

Erinevate väärtuste arvu leidmine

Korduvate väärtustega andmetabeli puhul võib sageli tekkida küsimus, kui palju on üldse erinevaid mõõdetud indiviide või kui palju on erinevaid mõõtmistulemusi. Üks võimalus on tekitada korduvate väärtusteta andmetabel (kas siis PivotTable või Data-sakil leiduva käsu Remove Duplicates abil) ja leida väärtuste arv selles. Teine võimalus on kasutada järgmist kavalat valemit.

Oletame, et väärtused, mille hulgast on vaja kokku lugeda unikaalsed, paiknevad lahtrites A2 kuni A20. Valem, mis arvutab (justnimelt arvutab, mitte ei loe kokku) erinevate väärtuste arvu, on siis kujul

= SUM( 1 / COUNTIF(A2:A20; A2:A20) )

NB! Tegu on massiivifunktsiooniga, st, et valemi rakendamiseks tuleb vajutada korraga kolme klahvi: Ctrl+Shift ja Enter.

Kui lahtriblokk, milles paiknevate unikaalsete väärtuste arvu arvutatakse, sisaldab puuduvaid väärtuseid, lõpeb eelneva valemi rakendamine veateatega #DIV/0!. Lahenduseks on kasutada täendavalt funktsiooni IFERROR, mis puuduvate väärtuste korral võtab nende arvuks lihtsalt nulli (vt ka Joonis 74):

= SUM( IFERROR( 1 / COUNTIF(A2:A20; A2:A20), 0 ) )

ja siis Ctrl+Shift ja Enter.
 

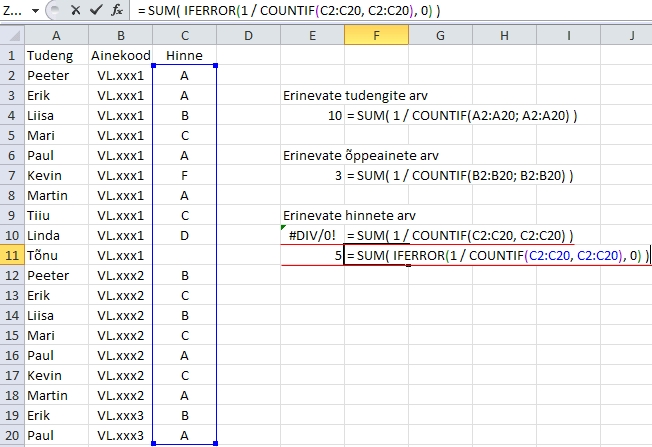
Joonis 74. Unikaalsete väärtuste kokku lugemine Excelis. NB! Valemi rakendamiseks tuleb korraga vajutada kolme klahvi: Ctrl+Shift ja Enter.
 

Mittelineaarne regressioonanalüüs funktsiooniga LINEST

Regressioonivõrrandeid, mis on argumentide suhtes lineaarsed, aga mille argumendid ise on argumenttunnuse mittelineaarsed funktsioonid - näiteks kolmandat järku polünoom

y = a + b₁*x + b₂*x² + b₃*x³

või astmefunktsioon kujul

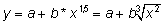
või logaritmfunktsioon kujul

y = a + b*ln(x)

- on Excelis võimalik hinnata

• protseduuriga Regression, aga seda eeldusel, et kõik argumentide mittelineaarsed funktsioonid on eelnevalt töölehele üksteise kõrvale välja arvutatud, ja
   
• graafiliselt punktdiagrammi ja sellele lisatud sobiva trendijoone abil - aga seda vaid mõnede spesiifiliste funktsioonide puhul (ülaltooduist on punktdiagrammile lisatav kolmandat järku polünoom ja logaritmfunktsioon) ning ilma võimaluseta hinnata parameetrite hinnangute täpsust ja statistilist olulisust.

Joonisel 75 on näidatud noormeeste kehamassi prognoosimine pikkuse alusel logaritmfunktsiooniga kasutades nii funktsiooni LINEST, protseduuri Regression kui ka graafilist lahendamist - tulemused on identsed, ainult sarnaselt eelnevalt vaadatud logaritmfunktsioonile LINEST kujul

= LINEST(B2:B51, LN(A2:A51), TRUE, TRUE)

• ei vaja erinevalt protseduurist Regression lahtrites A2:A51 paiknevate pikkuste logaritmi eelnevat välja arvutamist ning
• erinevalt graafilisest lahendusest on väljund rikkalikum, võimaldades täiendavalt testida ka hüpoteese regressioonivõrrandi statistilise olulisuse kohta (vastava teooria kohta vt pt 7.3 funktsiooni LINEST alapunkti).
   

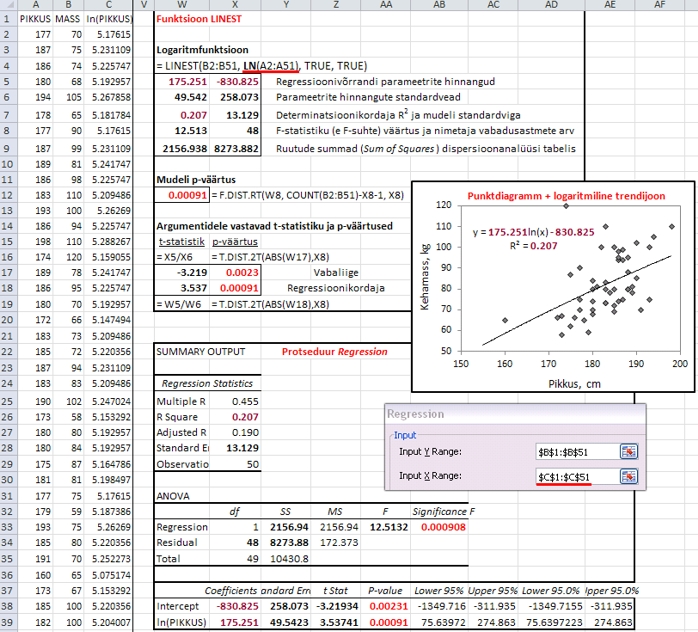
Joonis 75. Noormeeste kehamassi prognoosimine pikkuse alusel logaritmfunktsiooniga kasutades funktsiooni LINEST, protseduuri Regression ja graafilist lahendamist. Tumepunases paksus kirjas on kõigil kolmel meetodil hinnatavad parameetrid, mustas paksus kirjas vaid funktsiooni LINEST ja protseduuri Regression väljundis sisalduvad parameetrid, helepunases paksus kirjas on p-väärtused, mis sisalduvad protseduuri Regression väljundis, aga on arvutatavad ka funktsiooni LINEST väljastatavate suuruste alusel. NB! Erinevalt protseduurist Regression ei vaja funktsioon LINEST ja graafiline lahendamine tudengite pikkuse logaritmi välja arvutamist andmetabelisse.
 

Joonisel 76 on näidatud noormeeste kehamassi prognoosimine pikkuse alusel kuuppolünoomiga kasutades nii funktsiooni LINEST, protseduuri Regression kui ka graafilist lahendamist - tulemused on identsed, ainult funktsioonile LINEST kujul

= LINEST(D2:D51, A2:A51^{1,2,3}, TRUE, TRUE)

ei ole erinevalt protseduurist Regression vaja eraldi välja arvutada pikkuse ruutu ja kuupi ning erinevalt graafilisest lahendusest on väljund rikkalikum.

PS. Mingeid sisulisi järeldusi antud ülesande puhul teha ei maksa, sest mudel tervikuna on küll statistiliselt oluline (p = 0,008), aga ükski mudeli liige eraldi võetuna statistiliselt oluline pole (kõigi mudeli parameetrite puhul p > 0,6) ning ega varem vaadatud mudelitega (logaritmfunktsioon või peatükis 7.3 käsitletud lineaarne funktsioon) võrreldes prognoosi täpsus (R² ja mudeli standardviga) ka paremad pole - seega on antud mudel ilmselgelt liiga keerukas. Siinkohal on see ära toodud lihtsalt illustreerimaks funktsiooni LINEST võimalusi.
 

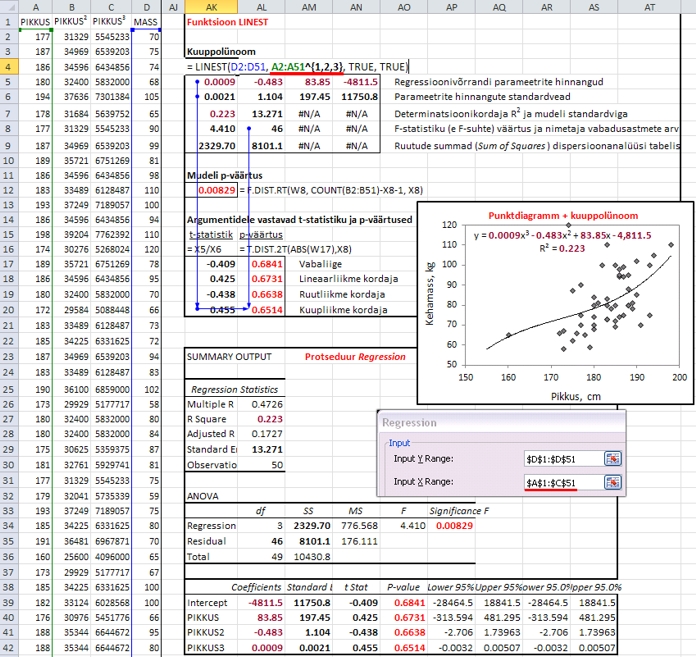
Joonis 76. Noormeeste kehamassi prognoosimine pikkuse alusel kuuppolünoomiga kasutades funktsiooni LINEST, protseduuri Regression ja graafilist lahendamist. Tumepunases paksus kirjas on kõigil kolmel meetodil hinnatavad parameetrid, mustas paksus kirjas vaid funktsiooni LINEST ja protseduuri Regression väljundis sisalduvad parameetrid, helepunases paksus kirjas on p-väärtused, mis sisalduvad protseduuri Regression väljundis, aga on arvutatavad ka funktsiooni LINEST väljastatavate suuruste alusel. NB! Erinevalt protseduurist Regression ei vaja funktsioon LINEST ja graafiline lahendamine tudengite pikkuse ruudu ja kuubi välja arvutamist andmetabeli eraldi veergudesse.
 

Astmefunktsiooni 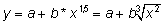parameetrid on funktsiooniga LINEST hinnatavad kujul

= LINEST(D2:D51, A2:A51^1.5, TRUE, TRUE)

(funktsioontunnuse y väärtused paiknevad lahtrites D2:D51 ja argumenttunnuse x väärtused lahtrites A2:A59; NB! eesti keele seadistuses Exceli puhul peab arvus 1.5 punkti asemel olema koma ja funktsiooni argumentide eraldajaks koma asemel semikoolon).