|
Kahefaktoriline dispersioonanalüüs
Kahefaktoriline
dispersioonanalüüs on Excelis teostatav
üksnes tasakaaluliste andmete korral, st juhul,
kui mõlema faktori kõigil tasemetel
on sooritatud ühepalju mõõtmisi.
Aga ka siis vaid ettemääratud mudeli kohaselt:
- protseduur
Anova: Two-Factor Without Replication eeldab,
et mõlema faktori kõigi tasemete kõigi
kombinatsioonide puhul on teostatud üksnes
üks mõõtmine, ja testib sedasi
vaid mõlema faktori peamõju statistilist
olulisust;
- protseduur
Anova: Two-Factor With Replications eeldab,
et mõlema faktori kõigi tasemete kõigil
kombinatsioonidel on teostatud võrdne ja
ühest suurem arv mõõtmiseid,
ja testib mõlema faktori peamõju pluss
nende koosmõju statistilist olulisust.
Seega
sobivad Exceli kahefaktorilise dispersioonanalüüsi
protseduurid vaid täpselt planeeritud ja läbi
viidud väikesemahuliste katsete andmete analüüsimiseks.
Kahefaktoriline
kordusteta dispersioonanalüüs
Kahefaktorilise
kordusteta dispersioonanalüüsi teostamiseks
Excelis tuleb (vt ka Joonis 68)
-
esitada analüüsitavad andmed risttabelina,
mis on jagatud ridadeks ühe ja veergudeks teise
faktori tasemete alusel ning kus igas lahtris paikneb
täpselt üks uuritava tunnuse väärtus,
-
rakendada protseduuri Anova: Two-Factor Without
Replication (Data-sakk -> Data Analysis), millele
tuleb ette anda
- sammul
1 loodud risttabel (Input Range),
- infovõrreldavate
gruppide nimede olemasolu kohta risttabeli esimeses
reas ja veerus (st, et nimed peavad olemas olema
kas mõlemat pidi või siis üldse
puuduma; Labels),
- olulisuse
nivoo F-statistiku kriitilise väärtuse
arvutamiseks (Alpha, vaikimisi 0,05),
- tulemustabelite
asukoht (Output options): samale töölehele
(Output Range), uuele töölehele
(New Worksheet Ply) või uude faili
(New Workbook).
Joonisel
68 on näidatud kahefaktorilise kordusteta dispersioonanalüüsi
teostamist protseduuriga Anova: Two-Factor Without
Replication, testimaks keskmise netopalga erinevust
maakondade ja aastate 2010-2012 vahel (andmed Statistikaameti
kodulehelt http://www.stat.ee).
Tulemuseks
on kaks tabelit, millest esimene sisaldab nii andmebaasi
ridu (antud näites maakondi) kui ka veerge (antud
näites aastaid) kirjeldavaid karakteristikuid.
Neist oluliseimad on aritmeetilised keskmised, mille
alusel saab vaadata, millised grupid (aastad ja maakonnad)
omavahel enam ja mis suunas erinevad. Antud juhul
on tulemused muidugi loomulikud - suurima keskmise
netopalgaga aastatel 2010-2012 on olnud Harju maakonna
töötajad (keskmine netopalk aastatel 2010-2012
751,67 eurot), millele järgneb Tartu maakond
(646,33 eurot), madalaim keskmine netopalk on olnud
Valga maakonnas (518,67 eurot). Uuritud aastate lõikes
on palk suurenenud - kui aastal 2009 oli keskmine
netopalk 536,07 eurot, siis aastal 2012 juba 590,67
eurot (mitte et see nüüd mingi eriti suur
arv oleks …).
Dispersioonanalüüsi
(ANOVA) tabelis vastab rida Rows maakonna mõjule
ja rida Columns aasta mõjule (sest just
niipidi oli algandmete tabel üles ehitatud).
Mõlema faktori mõju on statistiliselt
oluline (p < 0,001).
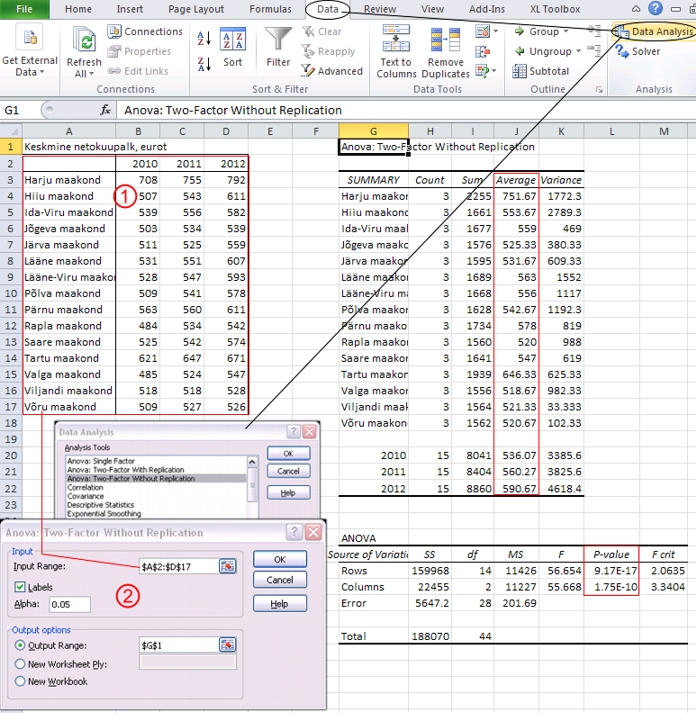
Joonis
68. Kahefaktorilise kordusteta dispersioonanalüüsi
teostamine protseduuriga Anova: Two-Factor Without
Replication ja selle tulemused, testimaks keskmise
netopalga erinevust maakondade ja aastate 2010-2012
vahel (andmed Statistikaameti kodulehelt http://www.stat.ee).
Kahefaktoriline
kordustega dispersioonanalüüs
Kahefaktorilise
kordustega dispersioonanalüüsi teostamiseks
Excelis tuleb (vt ka Joonis 69)
-
esitada analüüsitavad andmed risttabelina,
mis on jagatud ridadeks ühe ja veergudeks teise
faktori tasemete alusel ning kus igale faktorite
tasemete kombinatsionile vastab sama arv nö
korduvaid mõõtmisi, mis paiknevad
eri ridades faktorite samade tasemete sees,
-
rakendada protseduuri Anova: Two-Factor With
Replications (Data-sakk -> Data
Analysis), millele tuleb ette anda
- sammul
1 loodud risttabel (Input Range),
- mõõtmiste
arv (kordsus) reafaktori taseme kohta (Rows
per sample),
- infovõrreldavate
gruppide nimede olemasolu kohta risttabeli esimeses
reas ja veerus (st, et nimed peavad olemas olema
kas mõlemat pidi või siis üldse
puuduma, seejuures võivad reafaktori tasemete
nimed olla ka vaid iga taseme esimeses reas; Labels),
- olulisuse
nivoo F-statistiku kriitilise väärtuse
arvutamiseks (Alpha, vaikimisi 0,05),
- tulemustabelite
asukoht (Output options): samale töölehele
(Output Range), uuele töölehele
(New Worksheet Ply) või uude faili
(New Workbook).
Joonisel
69 on näidatud kahefaktorilise kordustega dispersioonanalüüsi
teostamist protseduuriga Anova: Two-Factor With Replications,
testimaks keskmise netopalga sõltuvust tööandja
(omaniku) liigist ja aastast (andmed Statistikaameti
kodulehelt http://www.stat.ee).
Tulemusena
väljastab Excel kirjeldavate statistikute tabelid
nii rea- kui ka veerufaktori kõigi tasemete
kohta. Antud juhul on näha, et kõrgeim
keskmine netopalk on olnud välismaa eraõiguslikust
isikust omaniku puhul (823,83 eurot), palju ei jää
maha keskmine netopalk ka riigi omandusega ettevõtetes
- 807,00 eurot. Madalaim keskmine netopalk aastatel
2010-2012 oli kohalike omavalitsuste omanduses - 553,58
eurot. Aastate lõikes on palk järjest
tõusnud.
Teisest
Exceli poolt väljastatud tabelist on näha,
et statistiliselt oluline erinevus keskmistes netopalkades
on nii omanike (reafaktor, Sample) kui ka aastate
(veerufaktor, Columns) vahel (mõlemal
juhul p < 0,001). Küll ei ole statistiliselt
oluline omaniku ja aasta koosmõju (Interaction,
p = 0,83), st et omanike vaheline erinevus
on samasugune sõltumata aastast nagu on ka
aastate vaheline erinevus samasugune sõltumata
omanikust.
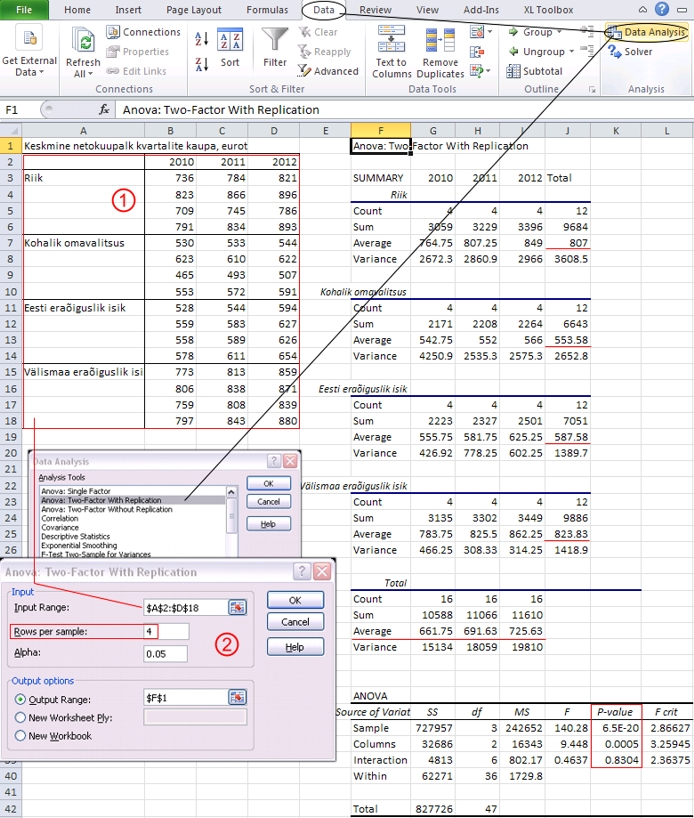
Joonis
69. Kahefaktorilise kordustega dispersioonanalüüsi
teostamine protseduuriga Anova: Two-Factor With
Replications ja selle tulemused, testimaks keskmise
netopalga sõltuvust tööandja (omaniku)
liigist ja aastast (andmed Statistikaameti kodulehelt
http://www.stat.ee).
|