Z-test

Keskväärtuse võrdlemine konstandiga

MS Exceli funktsioon Z.TEST testib normaaljaotuse ning teadaoleva dispersiooni (või suure valimi) eeldusel ühepoolset hüpoteesi kujul

H₀: μ ≤ konstant
H₁: μ > konstant

(μ on uuritava tunnuse keskväärtus).

Funktsioonile ZTEST tuleb ette anda (Joonis 32)

• Array - algandmete blokk (ilma tunnuse nimeta),
• X - konstant, millega võrdumist kontrollitakse,
• Sigma - populatsiooni teadaolev standardhälve (NB! võib ka puududa, siis arvutab Excel ise valimi standardhälbe valemiga STDEV.S ja kasutab seda).

Tulemusena väljastab Excel eelnevalt kursoriga määratud lahtrisse olulisuse tõenäosuse p väärtuse. Kui leitud p < 0,05, võib lugeda tõestatuks alternatiivse hüpoteesi H₁: uuritava tunnuse keskväärtus on võrreldavast konstandist suurem ja seda olulisuse nivool 0,05.

Näiteks kui eeldada, et esimese kursuse neidude pikkuse standardhälve on teadaolevalt 6,5 cm, siis testides hüpoteesi: esimese kursuse neidude keskmine pikkus on suurem, kui Eesti naiste keskmine pikkus 168 cm, on tulemuseks p-väärtus 0,11 (Joonis 33). Seega saab järeldada, et esimese kursuse neidude keskmine pikkus ei ole statistiliselt oluliselt suurem, kui Eesti naiste keskmine pikkus 168 cm (p = 0,11).
 

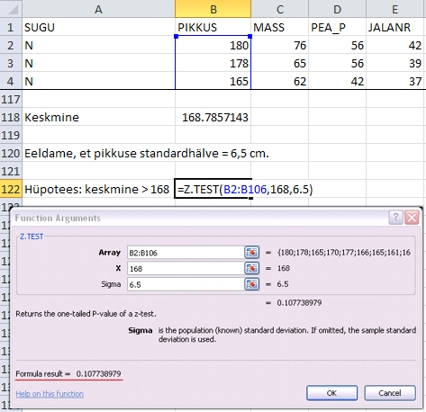
Joonis 33. Neidude keskmise pikkuse võrdlemine 168 sentimeetriga teadaoleva pikkuse standardhälbe 6,5 cm korral funktsiooniga Z.TEST.
 

Kuna funktsioon Z.TEST testib alati ühepoolset hüpoteesi: keskväärtus on konstandist suurem, on juhul, kui tegelik andmetest leitud keskmine on võrreldavast konstandist väiksem, tulemuseks kindlasti 0,05-st suurem p-väärtus.

Näiteks soovides võrrelda esimese kursuse neidude keskmist pikkust (mis antud andmete alusel on 168,8 cm) 170-ga, testib Z.TEST tegelikult seda, kas 168,8 > 170. Tulemuseks on p-väärtus 0,97 (Joonis 34) - esimese kursuse neidude keskmine pikkus ei ole statistiliselt oluliselt suurem 170-st. Mis on ka loomulik, sest tegelikult on neidude pikkus hoopis väiksem kui 170: 168,8 < 170.

Soovides testida ühepoolset hüpoteesi teistpidi: neidude keskmine pikkus on väiksem kui 170, piisab standardse normaaljaotuse sümmeetrilisuse tõttu nulli suhtes lihtsalt funktsiooni Z.TEST poolt väljastatud p-väärtuse ühest lahutamisest. Tulemuseks on p = 0,028 - neidude keskmine pikkus on statistiliselt oluliselt väiksem 170-st (Joonis 34).

Soovides testida kahepoolset hüpoteesi, piisab lihtsalt nö õiges suunas testitud ühepoolse hüpoteesi p-väärtuse kahega korrutamisest (Joonis 34). Ehk siis testides hüpoteesi: neidude keskmine pikkus erineb 170-st, on tulemuseks p = 0,056 - neidude keskmine pikkus ei ole statistiliselt oluliselt erinev 170-st.
 

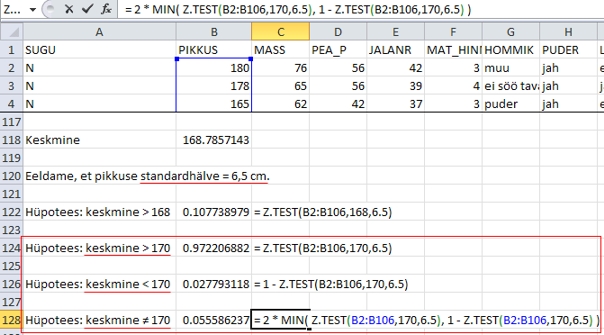
Joonis 34. Ühe- ja kahepoolsete hüpoteeside testimine funktsiooniga Z.TEST.
 

Kahe üldkogumi keskväärtuste võrdlemine teadaolevate dispersioonide korral

Kahe üldkogumi keskväärtuse võrdlemine teadaolevate dispersioonide korral on teostatav protseduuriga z-Test: Two Sample for means (Data-sakk -> Data Analysis).

Protseduuril tuleb ette anda (Joonis 35)

• mõlema valimi andmete blokid - Variable 1 Range ja Variable 2 Range (seejuures võivad andmed paikneda nii veerus kui ka reas),
• oletatav keskväärtuste erinevus (vaikimisi null) - Hypothesized Mean Difference,
• mõlema populatsiooni teadaolevad dispersioonid - Variable 1 Variance (known) ja Variable 2 Variance (known),
• kui andmete blokid sisaldavad esimeses reas/veerus nime, tuleb teha "linnuke" märgendi Labels ette,
• olulisuse nivoo (vaikimisi 0,05) - Alpha,
• tulemuste väljastamise asukoht (Output options): samale töölehele (Output Range), uuele töölehele (New Worksheet Ply) või uude faili (New Workbook).

NB! erinevalt funktsioonist Z.TEST, mille argumendiks oli populatsiooni standardhälve, tahab protseduur z-Test: Two Sample for means saada argumentidena ette populatsiooni dispersioone.

Joonisel 35 on näidatud spordiga tegelevate ja mittetegelevate esimese kursuse neidude keskmiste kehamasside võrdlemist protseduuriga z-Test: Two Sample for means. Kehamasside dispersiooniks sai mõlemas grupis võetud 100 kg² (oletame, et see on teada). Analüüsi tulemustest on näha, et spordiga tegelevate neidude kehamass on tegelikult hoopis kõrgem, kui spordiga mittetegelevatel neidudel - vastavalt 63,1 ja 60,7 kg - ju siis peab sportimiseks olema põhjus :) Siiski ei ole see erinevus statistiliselt oluline (p = 0,29).
 

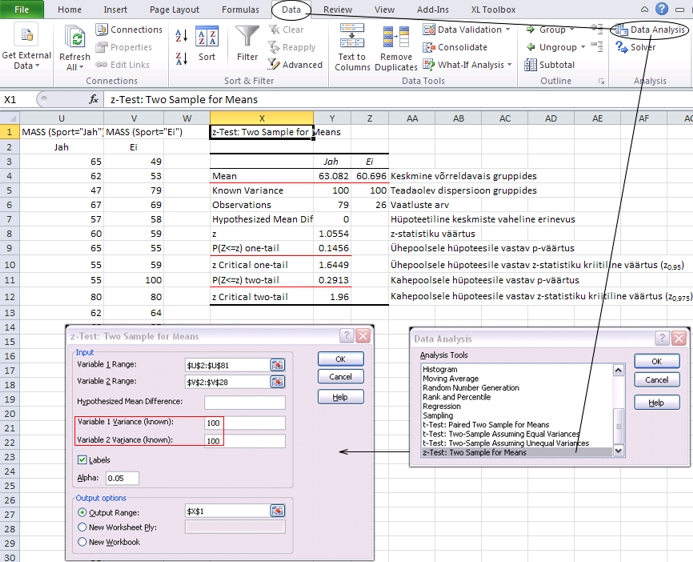
Joonis 35. Sportivate ja mittesportivate neidude keskmiste kehamasside võrdlemine protseduuriga z-Test: Two Sample for means.
 

Ühepoolse hüpoteesi testimisel võtab protseduur z-Test: Two Sample for means alati aluseks tegelikud keskmised ning testib, kas suurem keskmine on ka statistiliselt oluliselt suurem kui väiksem keskmine. Antud näite puhul testitakse siis, kas spordiga tegelevate neidude kehamass on kõrgem, kui spordiga mittetegelevate neidude kehamass - vastus on, et on küll, ainult et mitte statistiliselt olulisel määral (p = 0,15).

Märkus. Et tunnuste varieeruvust üldkogumis tavaliselt ei teata, siis leiab vaadeldud protseduur ka vähest praktilist rakendust.