|
Regressioonanalüüs
Solver'i abil
Solver
on Exceliga kaasa tulev lisamoodul optimeerimisülesannete
lahendamiseks. Menüüsakilt Data rakendatav
Solver võimaldab leida, millised ühtedes
lahtrites olevad parameetrite väärtused
kas minimiseerivad või maksimeerivad teises
lahtris paikneva, neist parameetritest sõltuva
funktsiooni väärtuse.
Regressioonivõrrandi
parameetrid hinnatakse klassikaliselt vähimruutude
meetodil. St, et võrrandi parameetriteks
valitakse sellised väärtused, mille korral
summaarne ruuterinevus tegelike ja prognoositud väärtuste
vahel on kõige väiksem. Seega on tegu
optimeerimisülesandega, mistap saab regressioonivõrrandi
parameetrite hindamiseks kasutada Solver'it.
Järgnevalt
on näidatud, kuidas rakendada Solver'it
lineaarse ja logistilise regressioonivõrrandi
parameetrite hindamiseks. Analoogselt on hinnatavad
ka eksponent- jm funktsioonide parameetrid.
NB!
Kui valik Solver menüü-sakil Data
puudub, tuleb järgida järgmist menüü-teekonda
ning optimeerimisülesannete lahendamise moodul
nimega Solver sisse lülitada:
File
-> Options -> Add-Ins -> Manage
|Excel Add-ins| [Go...] -> Solver.
Täpsemalt
Exceli Solver'i olemusest ja kasutamisest vt
http://www.solver.com/content/basic-solver-overview-and-example.
Solver'i
rakendamisest lineaarsete planeerimisülesannete
lahendamisel vt näiteks http://www.sauga.pri.ee/linplan/linplanfiles.html.
Regressioonanalüüsi
teostamisest Solver'i abil vt näiteks
http://chemlab.truman.edu/chemlab_backup/DataAnalysis/Excel_Files/AdvancedRegression.htm.
Lineaarse
regressioonivõrrandi parameetrid Solver'i
abil
Uuritava
tunnuse y väärtuste prognoosimiseks lineaarse
regressioonivõrrandi
y
= a + bx
abil
vajalike parameetrite a ja b hindamiseks
Solver'iga tuleb (Joonised 61A, 61B ja 61C)
- määrata
töölehel lahtrid regressioonivõrrandi
parameetrite a ja b tarvis ning kirjutada
sinna mingid algväärtused,
-
lisada andmetabeli kõrvale veerg uuritava
tunnuse prognoositud väärtuste
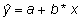 tarvis ning sisestada sinna valem arvutamaks välja
prognoose iga andmetabeli rea kohta kasutades sammul
1 määratud lahtrites olevaid parameetrite
algväärtuseid (NB! valem peab sisaldama
viiteid neile lahtritele, mitte kordajate arvulisi
väärtusi),
tarvis ning sisestada sinna valem arvutamaks välja
prognoose iga andmetabeli rea kohta kasutades sammul
1 määratud lahtrites olevaid parameetrite
algväärtuseid (NB! valem peab sisaldama
viiteid neile lahtritele, mitte kordajate arvulisi
väärtusi),
-
arvutada prognooside kõrvale välja prognoosivigade
ruudud
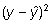 (nn ruutvead) ning
(nn ruutvead) ning
-
eraldi lahtrisse summaarne ruutviga - viimane
kujutab enesest optimeerimisülesande sihifunktsiooni,
mille väärtus on vaja vastavalt vähimruutude
meetodile minimiseerida,
-
käivitada Solver (Data-sakk ->
Solver) ning määrata avanenud aknas
- lahter,
milles paikneva valemi tulemuse suhtes soovite optimeerimist
läbi viia (lahter, milles paikneb sihifunktsioon;
Set Objective) - regressioonanalüüsi
puhul on selleks summaarne ruutviga,
- mida
soovitakse sihifunktsiooniga teha: maksimeerida
(Max), minimiseerida (Min) või
võtta võrdseks mingi väärtusega
(Value Of) - regressioonanalüüsi
puhul on eesmärgiks sihifunktsiooni, so summaarse
ruutvea, minimiseerimine,
- lahtrid,
milles paiknevate väärtuste muutmise teel
soovitakse sihifunktsiooni väärtust optimeerida
(By Changing Variable Cells) - regressioonanalüüsi
puhul on neiks muudetavateks väärtusteks
regressioonivõrrandi parameetrid a
ja b,
- vajadusel
määrata ka
-
lisakitsendused (Subject to the Constraints),
-
optimeerimisalgoritm (NB! regressioonanalüüsi
puhul tuleks valida meetod GRG Nonlinear),
-
luba negatiivseteks lahenditeks - selleks tuleb
ära võtta "linnuke" valiku
Make Unconstrained Variables Non-Negative
eest (NB! see on oluline koht Solver'i
rakendamisel regressioonivõrrandi parameetrite
hindamisel, sest erinevalt mitmetest planeerimise
ülesannetest regressioonivõrrandi
parameetrite puhul väärtuste positiivsuse
nõuet pole),
-
täpsustada optimeerimisalgoritmi tööd
(valik Options) - kui sooviks on vaid
summaarset ruutviga minimiseerivate regressioonivõrrandi
parameetrite välja arvutamine ja optimeerimisprotsessi
vahepealsed tulemused huvi ei paku, on mõttekas
võtta ära "linnuke" valiku
Show Iteration Results eest,
-
käivitada optimeerimisalgoritm vajutades nupule
Solve ning
-
lasta Excelil optimeerimisalgoritmi koondumise järel
säilitada töölehel Solver'i
poolt leitud parameetrite väärtused: Keep
Solver Solution.
Joonistel
61A, 61B ja 61C on illustreeritud Solver'i
rakendamist prognoosimaks noormeeste kehamassi nende
pikkuse abil lineaarse regressioonivõrrandiga.
Võrrandi
vabaliikme a ja regressioonikordaja b
algväärtusteks sammul 1 on võetud
vastavalt 0 ja 0,5. Miks need arvud? Lihtsalt niivõrd-kuivõrd
loogiline arutelu - kui pikkus on null, siis peaks
ka kehamass olema null (inimest pole), seega võiks
vabaliige olla null; ja kuna pikkuse ja kehamassi
vahel on ilmselt positiivne seos - mida pikem inimene,
seda enam ta kaalub - ja vaevalt iga lisasentimeeter
pikkuses kehamassile üle kilo lisab (aga mine
tea), siis võiks regressioonikordaja alglähendina
proovida mingit väikest positiivset arvu, näiteks
0,5 või 1.
Hinnatavate parameetrite algväärtuste muutmine
on ka üks võimalik tegutsemisvariant,
kui Solver algselt paika pandud väärtustest
alustades ei suuda lahendit leida.
Joonisel
61C on Solver'i tulemused esitatud kõrvuti
protseduuri Regression väljundiga. Tulemused
- nii regressioonivõrrandi parameetrite hinnangud
kui ka neile vastav vähim võimalik summaarne
ruutviga - on võrdsed.
Regressioonivõrrandi
parameetrite hinnangute usaldusväärsuse
ja statistlise olulisuse üle otsustamiseks vajalikud
arvutused on samuti võimalik läbi viia
Solver'iga saadud hinnangute jaoks, ainult
selleks peab teadma pisut põhjalikumalt vastavate
analüüside matemaatilist tausta. Soovi korral
saab abi näiteks artiklist:
Harris, D. C. (1998). Nonlinear Least-Squares Curve
Fitting with Microsoft Excel Solver. Journal of Chemical
Education, 75, 119-121 (http://jchemed.chem.wisc.edu/Journal/Issues/1998/Jan/PlusSub/V75N01/p119.pdf).
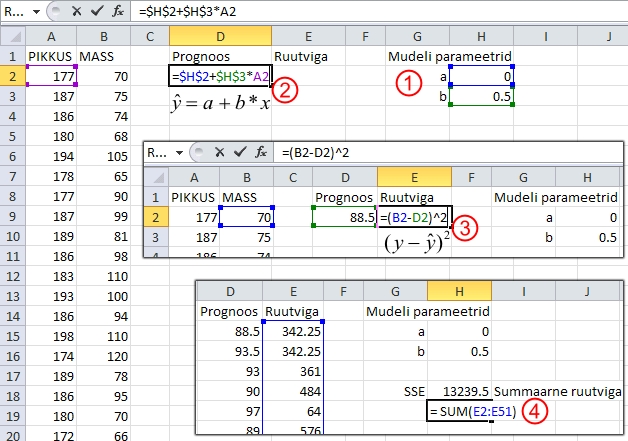
Joonis
61A. Noormeeste kehamassi prognoosimine nende pikkuse
alusel - mudeli parameetrite ja neist sõltuva,
Solver'i abil minimiseeritava, summaarse ruutvea
vahelise seose esitamine valemite abil.
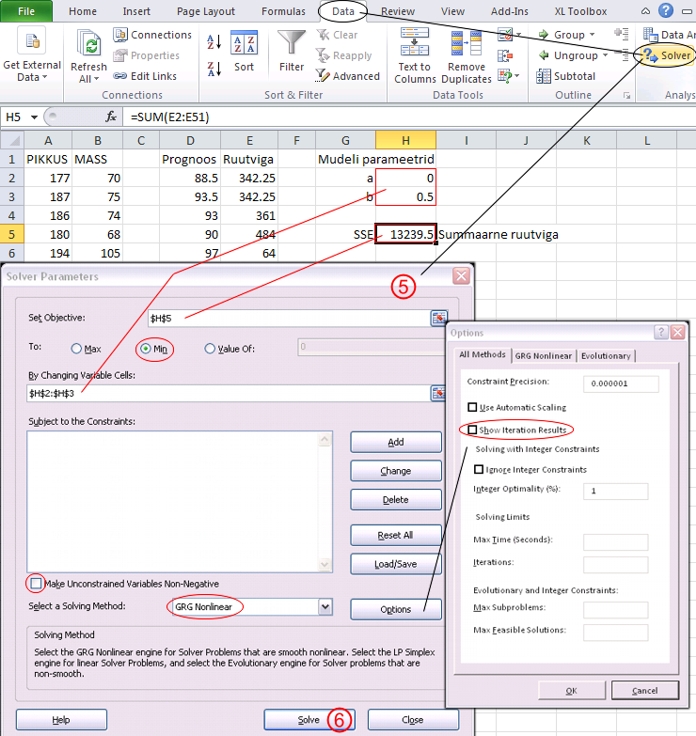
Joonis
61B. Noormeeste kehamassi prognoosimine nende pikkuse
alusel - mudeli parameetrite hindamine Solver'i
abil.
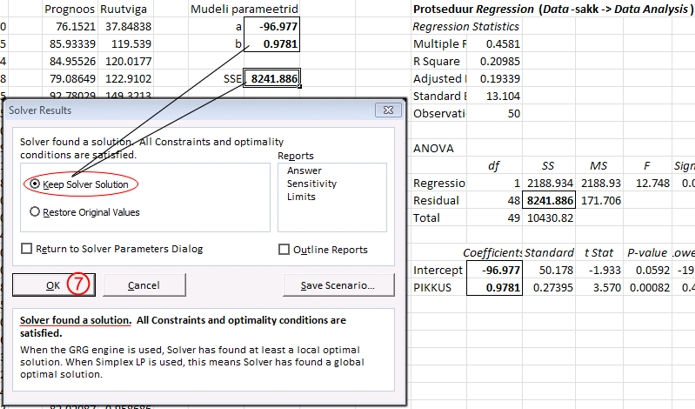
Joonis
61C. Noormeeste kehamassi prognoosimine nende pikkuse
alusel - Solver'i abil hinnatud parameetrite
väärtused; võrdluseks on esitatud
sama ülesande lahendamisel protseduuriga Regression
saadud tabelid.
Logistilise
regressioonivõrrandi parameetrid Solver'i
abil
Eelnevalt
lineaarse regressioonivõrrandi parameetrite
hindamiseks kasutatud metoodika on rakendatav ka mittelineaarsete
regressioonivõrrandite puhul, ainuke erinevus
on sammul 2 kasutatavas prognoosivõrrandis.
Järgnevalt
on lühidalt näidatud, kuidas hinnata logistilise
regressioonivõrrandi
p
= P(y=1|x) = exp(a + bx)/[1
+ exp(a + bx)] = 1 / [1 + exp(-a
- bx)
ehk
logit-funktsiooni
ln[p/(1-p)]
= logit(p) = a + bx
parameetreid
Solver'i abil. Modelleeritavaks on siinkohal
uuritava sündmuse y toimumise tõenäosus
p = P(y=1).
Täpsemalt
logistilise regressiooni olemusest vt vastavaid lehekülgi
õpiobjektis "Binaarsete tunnuste analüüs"
(http://ph.emu.ee/~ktanel/bin_tunnuste_analyys/).
Konkreetse
näitena on vaatluse all tudengi meheks olemise
tõenäosuse prognoosimine nädalas
keskmiselt tarbitava õllekoguse alusel (NB!
uuritav tunnus - antud näites sugu - peab olema
kodeeritud arvuliseks väärtustega 0 ja 1).
Ülesande lahendamiseks tuleb (vt ka Joonis 62)
-
määrata töölehel lahtrid regressioonivõrrandi
parameetrite a ja b tarvis ning kirjutada
sinna mingid algväärtused - viimaste väljamõtlemisel
võib arvestada, et
- vabaliige
a näitab meheks olemise tõenäosust
juhul, kui tudeng üldse õlut ei joo,
ja selleks võtta näiteks väärtuse
0 (või 0,25 või … mingi väärtuse
nulli ja ühe vahel),
- regressioonikordaja
b näitab meheksolemise logaritmilise
šansi muutust kordades, kui tarbitav õllekogus
suureneb ühe liitri võrra, ja ilmselt
on selle väärtuse näol tegu mingi
ühest pisut suurema arvuga, näiteks 1,1
- šanss olla mees suureneb e1,1=3
korda, kui nädalas tarbitav õllekogus
suureneb 1 liitri võrra (joonisel 62 esitatud
näites on alglähendiks võetud küll
0,1, aga nagu näha, koondub hindamisprotsess
ka sellise sisuliselt mitte kõige õigema,
aga matemaatiliselt siiski suhteliselt sobiva alglähendi
puhul),
-
lisada andmetabeli kõrvale veerg uuritava
tunnuse prognoositud väärtuste
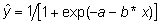 tarvis
ning sisestada sinna valem arvutamaks välja
prognoose iga andmetabeli rea kohta kasutades sammul
1 määratud lahtrites olevaid parameetrite
algväärtuseid (x selles valemis
on õllekogus), tarvis
ning sisestada sinna valem arvutamaks välja
prognoose iga andmetabeli rea kohta kasutades sammul
1 määratud lahtrites olevaid parameetrite
algväärtuseid (x selles valemis
on õllekogus),
-
arvutada prognooside kõrvale välja prognoosivigade
ruudud
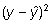 (nn ruutvead) ning
(nn ruutvead) ning
- eraldi
lahtrisse summaarne ruutviga,
-
käivitada Solver (Data-sakk ->
Solver) ning
- anda
ette minimiseeritavat summaarset ruutviga sisaldav
lahter (Set Objective),
- määrata
optimeerimise suunaks minimiseerimine (Min),
- anda
ette regressioonivõrrandi parameetrite algväärtuseid
sisaldavad lahtrid (By Changing Variable Cells),
- määrata
optimeerimisalgoritmiks GRG Nonlinear,
- võtta
ära "linnuke" valiku Make Unconstrained
Variables Non-Negative eest (sest regressioonivõrrandi
parameetrite puhul väärtuste positiivsuse
nõuet pole),
- võtta
ära "linnuke" valiku Options
-> Show Iteration Results eest (kui ei
ole just soovi igal iteratsiooni sammul leitud hinnanguid
eraldi uurida),
-
käivitada optimeerimisalgoritm vajutades nupule
Solve ning
-
lasta Excelil optimeerimisalgoritmi koondumise järel
säilitada töölehel Solver'i
poolt leitud parameetrite väärtused: Keep
Solver Solution.
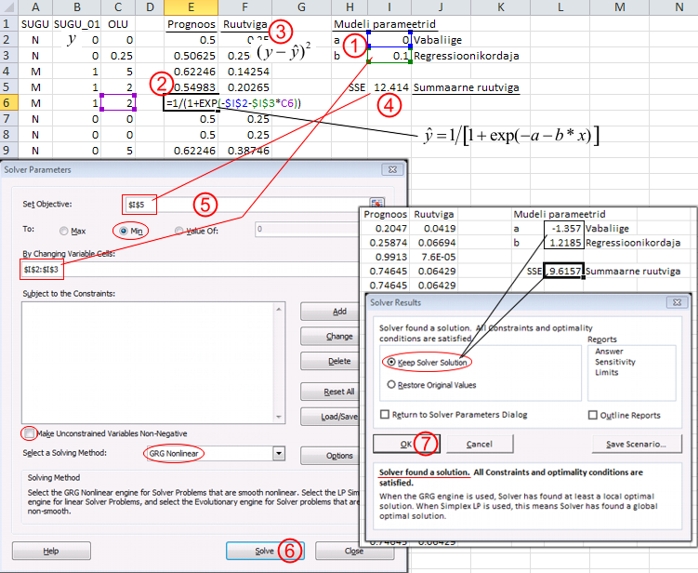
Joonis
62. Logistilise regressioonivõrrandi parameetrite
hindamine Solver'iga prognoosimaks tudengi
meheks olemise tõenäosust nädalas
keskmiselt tarbitava õllekoguse alusel.
Joonisel
62 esitatud analüüsi tulemuste kohaselt
on tudengi meheks olemise tõenäosus hinnatav
valemist
P(Mees)
= 1 / [1 + exp(1,357 - 1,22*Õlu)
ja
šanss olla mees suureneb e1,22 = 3,38 korda,
kui nädalas tarbitav õllekogus suureneb
1 liitri võrra.
Joonisel
63 on sama seos kujutatud graafiliselt (kuidas taolist
joonist Excelis konstrueerida vt vastavat õpetust
õpiobjektis "MS Excelile mitteomased andmeanalüüsil
kasutatavad joonised", http://ph.emu.ee/~ktanel/joonised_excelis/).
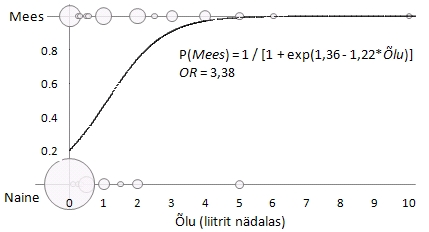
Joonis
63. Logistilise regressioonivõrrandi graafik
prognoosimaks tudengi meheks olemise tõenäosust
nädalas keskmiselt tarbitava õllekoguse
alusel (ringid vastavad erinevatele õllekogustele
ja ringi suurus tudengite arvule, pidev must joon
on logistilise regressioonivõrrandi graafik).
|