Fisheri täpne test

Fisheri täpne test on alternatiiv χ²-testile. Fisheri täpne test annab, nagu nimigi ütleb, täpse olulisuse tõenäosuse p väärtuse ning on tänu oma töömahukusele rakendatav eelkõige väikeste valimite korral (suurte valimite korral annab piisavalt täpse tulemuse ka χ²-test).

Kuigi Excelis puuduvad vahendid Fisheri täpse testi teostamiseks ja reaalseteks arvutusteks on mõttekam kasutada mõnda statistikapaketti või mõnda statistilisi analüüse teostavat internetilehekülge (vt vastavat lehekülge binaarsete tunnuste analüüsi käsitlevas õpiobjektis: http://www.eau.ee/~ktanel/bin_tunnuste_analyys/pt27.php), on alljärgnevalt nö pedagoogilistel kaalutlustel siiski näidatud ka Fisheri täpse testi teostamist Excelis(Joonis 66).

1. Fisheri täpse testi korral leitakse esmalt nagu χ²-testi puhulgi andmetele vastav e empiiriline sagedustabel.
    
2. Seejärel pannakse kirja kõik sellised alternatiivsed sagedustabelid, mis erineva "sisu" korral annavad tulemuseks ikkagi samad rea- ja veerusummad. Excelis on selliseks tegevuseks lihtsaim variant

• otsida empiirilises sagedustabelis üles väikseimale rea- ja veerusummale vastav lahter ning avaldada ülejäänud sagedused valemina antud lahtriväärtusest ning rea- ja veerusummadest (Joonisel 66 on vastav lahter värvitud oranžiks),
• teha taolisest empiirilisest sagedustabelist k koopiat, kus k = min(n_i.,n_.j), n_i. ja n_.j on vastavalt i. rea ja j. veeru summad (fikseeritud rea- ja veerusummade puhul on erinevaid sagedustabeleid min(n_i.,n_.j)+1 tükki, koopiad on mõtet teha üks vähem, sest empiiriline sagedustabel on juba olemas), ning
• muuta kopeeritud tabelites väikseimale rea- ja veerusummale vastavas lahteris paiknevat väärtust 0-st min(n_i.,n_.j)-ni - eeldusel, et teiste sageduste arvutamiseks sisaldas tabel vastavaid valemeid, arvutatakse need kõik automaatselt.

3. Kõigi leitud sagedustabelite saamise tõenäosus fikseeritud rea- ja veerusummade puhul eeldusel, et kõik katseobjektid/indiviidid jaotuvad tabelisse juhuslikult (so tunnuste sõltumatuse korral), on arvutatav hüpergeomeetrilise jaotuse tõenäosusfunktsioonist kujul

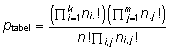, n! = n × (n-1) × … × 2 × 1,

kus n on vaatluste koguarv, nij sagedustabeli i. reas ja j. veerus paiknev sagedus ning n_i. ja n_.j vastavalt i. rea ja j. veeru summad (n! on arvu n faktoriaal, mis Excelis on leitav funktsiooniga FACT). Juhul, kui mõlemad uuritavad tunnused on binaarsed, esitatakse kahemõõtmeline sagedustabel sageli kujul

	Juht	Kontroll	Kokku
Eksponeeritud	a	b	a+b
Mitteeksponeeritud	c	d	c+d
Kokku	a+c	b+d	n = a+b+c+d

ning tõenäosus taolise tabeli saamiseks fikseeritud rea- ja veerusummade puhul juhuslikult avaldub valemiga

p_tabel = [(a+b)!(c+d)!(a+c)!(b+d)!] / [n!a!b!c!d!].

4. Viimaks liidetakse kokku empiirilise ning sellest ekstreemsemate (vähemtõenäolises suunas valitud) sagedustabelite esinemistõenäosused - tulemuseks on ühepoolsele hüpoteesile vastav olulisuse tõenäosus (p-väärtus);
   kahepoolsele hüpoteesile vastava olulisuse tõenäosuse saab, summeerides kõik empiirilise sagedustabeli esinemistõenäosusega võrdsed või sellest väiksemad tabeliste tõenäosused. Mõnikord leitakse kahepoolsele hüpoteesile vastav olulisuse tõenäosus ka korrutades ühepoolsele hüpoteesile vastava p-väärtuse lihtsalt kahega.
    

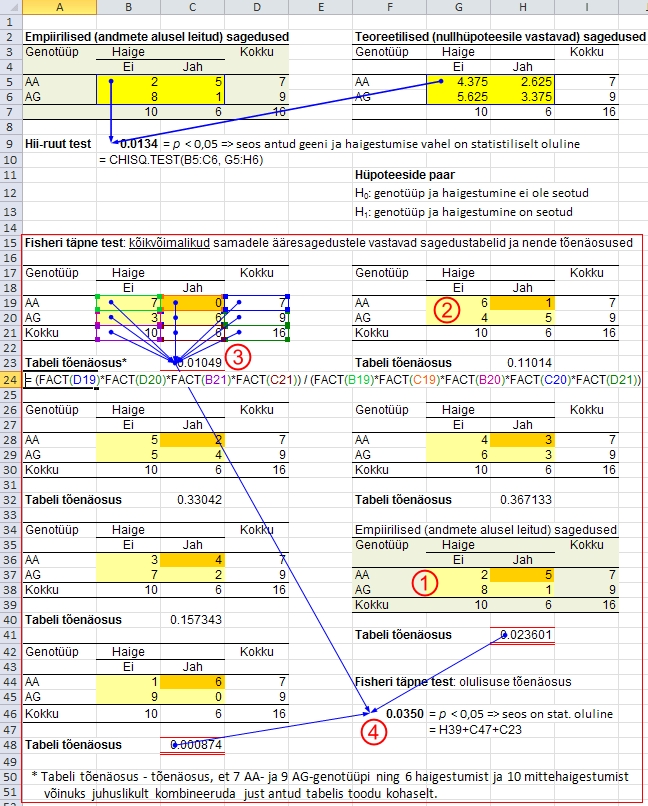
Joonis 66. Fisheri täpse testi teostamine Excelis. Võrdluseks on ära toodud ka χ²-testi teostus ja tulemus. Empiiriline andmetabel on varjutatud taustaga, selle esinemistõenäosusega võrdsed ja väiksemad tõenäosused, mille summana kujuneb Fisheri täpse testi p-väärtus, on allajoonitud punase topeltjoonega.