|
Hüpoteeside
kontrollimise üldskeem Excelis
Sõltuvalt
andmete olemusest ja kontrollitava hüpoteesi
tüübist on MS Excelis mitmeid erinevaid
võimalusi ühe ja kahe üldkogumi võrdlemiseks.
Skeem joonisel 31 annab lühiülevaate, millist
funktsiooni või protseduuri millal kasutada.
NB!
Paljudes statistikaõpikutes ja ka algselt antud materjalis esitatud VÄIDE, et kahe üldkogumi keskmiste võrdlemisel t-testiga
(sõltumatute valimite korral) tuleb esmalt võrrelda
F-testiga dispersioone otsustamaks, kas varieeruvus võrreldavates gruppides on ühesugune või mitte, ning selle alusel otsustada, kas kasutada nn teist või kolmandat tüüpi t-testi,
EI OLE ÕIGE. F-test sobib küll dispersioonide võrdlemiseks, aga otsus t-testi valikuks on õigem teha, lähtudes sisulistest teadmistest:
kui on alust eeldada varieeruvuse võrdsust (on teada, et varieeruvus ei erine), siis tuleks kasutada võrdset varieeruvust eeldavat nn teist tüüpi t-testi,
kui varieeruvuse võrdsuse või erinevuse kohta infot (eelteadmist) ei ole, tuleks kasutada nn kolmandat tüüpi (mittevõrdse varieeruvusega arvestavat) t-testi, ja seda sõltumata F-testi tulemusest!
Tänud Märt Mölsile ülaltoodule tähelepanu juhtimise eest.
Lisaks
tuleb arvestada, et kõik Excelis leiduvad ühe
ja kahe üldkogumi võrdlemise vahendid
eeldavad, et uuritav(ad) tunnus(ed) on normaaljaotusega
või on andmeid palju. Mitteparameetriliste,
normaaljaotust mitte-eeldavate testide teostamiseks
Excelis sisseehitatud vahendid puuduvad. Siiski on
mõnede mitteparameetriliste testide läbiviimine
Excelis võimalik - kas siis testide aluseks
olevate arvutuste samm-sammulise teostamise või
spetsiaalsete lisamoodulite abil (vt peatükk
5.6).
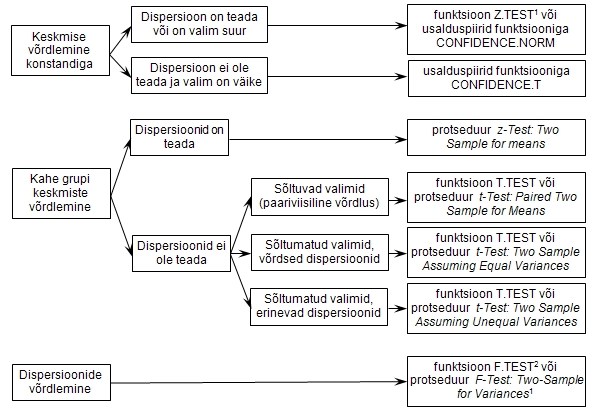
Joonis
31. Ühe ja kahe grupi võrdluse üldskeem
MS Excelis; 1 funktsioon Z.TEST ja protseduur
F-Test: Two-Sample for Variances teostavad
üksnes ühepoolse testi, 2 funktsioon F.TEST
aga vaid kahepoolse testi.
|