Dispersioonikomponentide hindamine -> REML-meetod

REML-meetod sobib dispersioonikomponentide hindamiseks ükskõik millise dispersioonistruktuuriga mudelite korral, kusjuures tasakaalulise traditsioonilise segamudeli korral on dispersioonikomponentide REML-hinnangud võrdsed ANOVA-hinnangutega. Lühend REML tähendab kitsendatud e jääkide e vähendatud suurima tõepära meetodit (REstricted e REsidual e REduced Maximum Likelihood method) ja baseerub nagu suurima tõepära meetodid ikka mingi teoreetilise jaotuse tõepärafunktsioonil. Üldise lineaarse mudeli 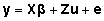(4) korral on selleks teoreetiliseks jaotuseks normaaljaotus -- . 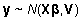Kitsendatud suurima tõepära meetodi idee seisneb selles, et kuigi üldine lineaarne mudel sisaldab kaht tüüpi hinnatavaid parameetreid -- fikseeritud faktorite efekte ja juhuslike faktorite dispersiooniparameetreid -- püütakse viimaste hindamiseks teisendada esialgset mudelit kujule, kus juhuslike faktorite mõjudest tingitud varieeruvus oleks sama, aga fikseeritud faktorite mõju võrduks nulliga. Sellisel juhul on kogu arvutusprotsess suunatud dispersioonikomponentide hindamisele, mis peaks garanteerima täpsemad hinnangud võrreldes tavalise suurima tõepära meetodiga (ML, Maximum Likelihood method), mis hindab samaaegselt nii fikseeritud faktorite mõjusid kui ka dispersioonikomponente. Mudeli (4) teisendust võib esitada korrutisena

,

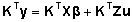kus maatriks K on defineeritud selliselt, et 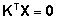, mistõttu

.

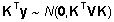Teisendatud mudeli vasakut poolt 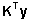võib mõista ka kui fikseeritud efektide poolt kirjeldamata jäänud osa uuritavast tunnusest y e erinevust (jääki) fikseeritud efektide poolt ärakirjeldatu ja uuritava tunnuse y tegelike väärtuste vahel (siit ka nimetus REsidual ML method).

REML-meetodi korral maksimeeritakse teisendatud uuritava tunnuse logaritmiline tõepärafunktsioon

,

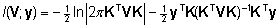(25)

dispersiooniparameetrite suhtes, võttes selleks funktsioonist (25) esimest järku osatuletise hinnatava parameetri suhtes, võrdsustades tulemuse nulliga ning lahendades -- tulemuseks ongi dispersiooniparameetri REML-hinnang. Üldjuhul ei ole dispersioonikomponentide hinnangute analüütiline leidmine võimalik, logaritmilise tõepärafunktsiooni maksimeerimise tulemusena saadakse keeruline maatriksvõrdus

,

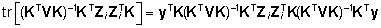kus mudeli dispersiooniparameetrid sõltuvad üksteisest ja ka juhuslike faktorite realiseerunud väärtustest (maatri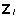ks koosneb i.-le juhuslikule faktorile vastavatest plaanimaatriksi Z veergudest). Üksikute parameetrite hinnangute leidmiseks kasutatakse ligikaudseid järkjärgulise lähendamise e iteratsioonimeetodeid: algselt (nn nullsammul) antakse mudeli parameetritele mingid algväärtused, neist lähtuvalt leitakse 1. sammul kõigi parameetrite uued hinnangud, seejärel lähtutakse 2. sammul parameetrite hinnangute arvutamisel juba 1. sammul leitutest jne -- igal järgneval sammul kasutatakse eelmisel sammul leitud hinnanguid; protsess koondub parameetrite lõplikeks hinnanguteks, kui mingil sammul leitud hinnangute erinevus eelneval sammul leitutest on piisavalt väike. Algoritme, mida sellisel ligikaudsel arvutamisel kasutatakse, on jälle rohkem kui üks -- mõni neist koondub väiksema, mõni suurema arvu sammude järel; teisalt ei pruugi enamasti kiiremini koonduvad algoritmid mõnel juhul üleüldse koonduda -- kõik see teeb dispersioonikomponentide hindamise veel keerulisemaks.

Põhjalikuma käsitluse dispersioonikomponentide hindamisest leiab magistritööst
Kaart, T. (1997). Dispersioonikomponentide ja päritavuskoefitsiendi hindamine loomapopulatsioonides. Magistritöö. TÜ matemaatikateaduskond, matemaatilise statistika instituut.