|
Täisastakuga
ja mitte täisastakuga mudelid, reparametriseerimis-tingimused
Üldine
lineaarne mudel on täisastakuga, kui täisastakuga
(kõik read-veerud lineaarselt sõltumatud,
pööratav) on tema plaanimaatriksi transponeeritud
maatriksi ja plaanimaatriksi enese korrutismaatriks,
näiteks 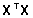 .
Nagu järgmisest peatükist
nähtub, kujutab just taoline korrutismaatriks
enesest mudeli parameetrite hindamiseks konstrueeritud
võrrandi kordajatemaatriksit. .
Nagu järgmisest peatükist
nähtub, kujutab just taoline korrutismaatriks
enesest mudeli parameetrite hindamiseks konstrueeritud
võrrandi kordajatemaatriksit.
Mudeli
parameetrid on üheselt hinnatavad üksnes
täisastakuga mudeli korral, sest vaid siis leidub
kasutataval kordajatemaatriksil ühene pöördmaatriks;
mitte-täisastakuga mudeli korral on erinevaid
parameetrite hinnanguid palju (teoreetiliselt lõpmatu
arv).
Tavalise
fikseeritud mudeli (2) korral
piisab mudeli parameetrite üheseks hinnanguks
ka plaanimaatriksi enese veergude lineaarsest sõltumatusest.
Täisastakuga on näiteks regressioonanalüüsi
mudel, sest plaanimaatriksi ühtedest koosnev
vabaliikmele vastav veerg pole üldjuhul mingi
lineaarkombinatsiooni tulemusena teisendatav argumenttunnuse
väärtuste veeruks.
Näide
7. Püstitades näite
2 alusel lihtsa lineaarse regressioonimudeli
prognoosimaks tallede võõrutusmassi
võõrutusvanuse abil, saame regressioonivõrrandi
maatrikskujul
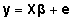 , ,
kus
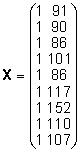 ja
ja 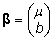 . .
Plaanimaatriksi
X veeruastak on 2, sest vabaliikmele ja regressioonikordajale
vastavad veerud on lineaarselt sõltumatud,
ja seega on parameetervektor 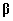 üheselt hinnatav.
üheselt hinnatav.
Täisastakuga
pole aga dispersioonanalüüsi mudel, sest
näiteks mistahes faktori kõigile tasemetele
vastavate veergude summeerimine annab tulemuseks ühtedest
koosneva vabaliikmele vastava veeru. Seega pole ka
dispersioonanalüüsi korral mudeli parameetrite
ühene hindamine võimalik. Lahenduseks
on hinnata mudeli parameetrite funktsioone, mis on
üheselt hinnatavad (nn hinnatavad funktsioonid
- estimable functions, vt pt
6.2) või kasutada mudeli parameetrite reparametriseerimist.
Viimane tähendab parameetritele mingi lisakitsenduse
rakendamist, mille all võib mõista näiteks
iga faktortunnuse viimase taseme mõju nulliga
võrdsustamist ja teiste tasemete mõjude
hindamist selle suhtes (kasutab näiteks statistikapakett
SAS ja kasutatakse ka antud õppevahendi järgnevais
näidetes) või traditsioonilisema reparametriseerimistingimusena
iga faktori mõjude summa nulliga võrdsustamist.
Seejuures peab selliseid lisakitsendusi olema sama
palju, kui on plaanimaatriksis lineaarselt sõltuvaid
veerge.
Näide
8. Mudel (1) näites 2
ei ole täisastakuga, sest plaanimaatriksi

veeruastak
on 6, mis on väiksem maatriksi X veergude
arvust (9) -- veergude lineaarne sõltuvus
ilmneb selles, et kõigi diskreetsete faktorite
korral annavad neile vastavad plaanimaatriksi veerud
summeeritult esimese, vabaliikmele vastava ühtedest
koosneva veeru.
Faktorite
mõjude üheseks hindamiseks on vajalik
teatud kitsenduste püstitamine. Näiteks
võime nõuda kõigi faktorite
korral nende mõjude summa nulliga võrdumist
(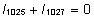 , ,
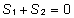 , ,
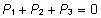 )
või siis iga faktori viimase efekti nulliga
võrdumist ( )
või siis iga faktori viimase efekti nulliga
võrdumist (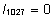 , ,
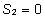 , ,
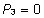 ). ).
|