|
Vaatluste
keskväärtused ja kovariatsioonistruktuur segamudeli
korral
Segamudeli
(4) korral tuleb arvesse võtta
ka juhuslike efektide keskväärtust ja varieeruvust.
Analoogselt juhuslike vigadega eeldatakse ka juhuslike
faktorite mõjude keskväärtuste nulliga
võrdumist: 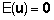 .
Seetõttu jääb uuritava tunnuse keskväärtus
endiselt määratuks üksnes fikseeritud
mõjude poolt: .
Seetõttu jääb uuritava tunnuse keskväärtus
endiselt määratuks üksnes fikseeritud
mõjude poolt:
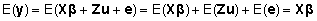 . .
Arvestades
dispersioonide defineerimisel ka juhuslike mõjude
varieeruvusega, saame, et
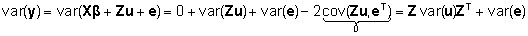 . .
Eelnevas
võrduste reas on eeldatud, nagu üldiste
lineaarsete mudelite teoorias tavaks, et faktorite
mõjud ja juhuslikud vead on sõltumatud:
 . .
Tuues
sisse tähistused 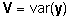 , ,
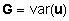 ja ja
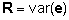 ,
saame segamudeli (4) keskväärtused
ja kovariatsioonistruktuuri määrata maatriksitena ,
saame segamudeli (4) keskväärtused
ja kovariatsioonistruktuuri määrata maatriksitena
ja
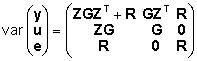 . . |
(8)
|
Traditsioonilises
segamudelis eeldatakse, et nii kõik uuritavad
objektid objektid kui ka kõik juhuslikud efektid
on omavahel sõltumatud, mistõttu on
nii jääkdispersioonimaatriks R kui
ka juhuslike efektide dispersioonimaatriks G
diagonaalmaatriksid:
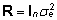 , , |
(9)
|
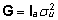 , , |
(10)
|
siin
n tähistab uuritavate objektide arvu ja
a juhusliku faktori tasemete arvu (enam kui
ühe juhusliku faktori korral on maatriks G
blokkdiagonaalne -- igale faktorile vastab tema tasemete
arvule vastava dimensiooniga diagonaalmaatriks).
Dispersioone
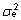 ja ja
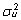 valemeis
(9) ja (10) nimetatakse dispersioonikomponentideks
(variance components), sest nad kujutavad enesest
vaatluste dispersiooni komponente: valemeis
(9) ja (10) nimetatakse dispersioonikomponentideks
(variance components), sest nad kujutavad enesest
vaatluste dispersiooni komponente: 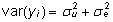 . .
Näide
5. Paneme kirja mudeli (5)
kovariatsioonimaatriksid (isade mõjusid käsitleme
juhuslike efektidena).
Vastavalt
valemitele (9) ja (10) saame, et
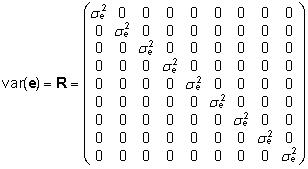
ja 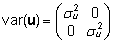 . |
(11)
|
Valemist
(8) järeldub, et 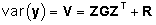 ,
seega ,
seega
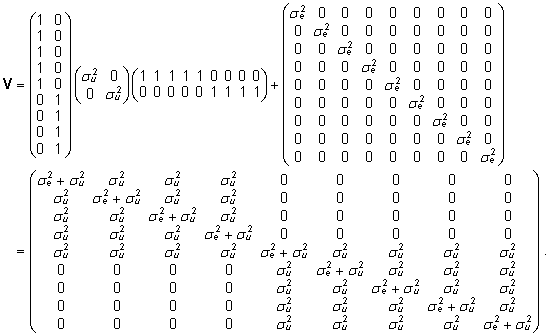
Viimasest
maatriksist ilmneb ka, et vaatluste dispersioonid
esituvad summana 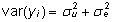 ja kovariatsioonid kujul
ja kovariatsioonid kujul

Märkus:
käsitledes isade mõjusid fikseeritutena,
avaldub vaatluste dispersioonimaatriks seosena (6):
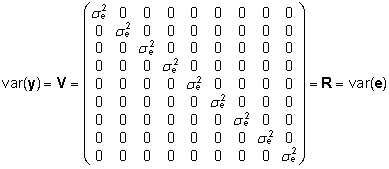 , ,
millest
omakorda järeldub, et 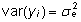 ja
ja 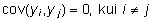 . .
|