Hinnatavad funktsioonid

Olgugi, et üldjuhul parameetervektor 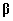ise ei ole üheselt hinnatav, on seda hulk tema elementide lineaarkombinatsioone . Viimaseid nimetatakse hinnatavateks funktsioonideks (estimable functions). Hinnatavuse olulisemad omadused lineaarsete mudelite korral on, et

1. vabaliige 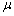ei ole üheselt hinnatav (va regressioonanalüüsi korral);
2. erinevused ühe faktori tasemete vahel on üheselt hinnatavad tingimusel, et mudelis puuduvad selle ja teiste faktorite vahelised interaktsioonid ning uuritava faktori tasemete mõjud ei kattu mõne teise faktori tasemete mõjudega;
3. sisulist tähendust omavad üksnes hinnatavate funktsioonide väärtused.

Näide 10. Et tallede võõrutusmassi mõjutavate faktorite tasemete hinnangute ei ole üheselt hinnatavad, saame hinnangutele 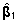(18) lisaks leida suure hulga erinevaid hinnanguid. Näiteks järgmised hinnangute vektorid on saadud kasutades erinevaid reparametriseerimistingimusi või rakendades erinevaid üldistatud pöördmaatrikseid valemis (16):

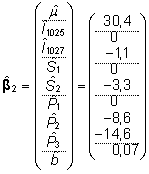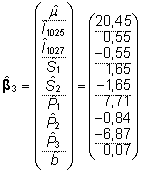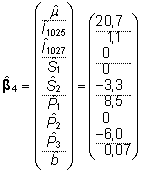, , jne.

Hinnatavad funktsioonid on näiteks

,

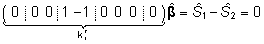mis hindab sugude vahelist erinevust ja on sama väärtusega mistahes parameetrite hinnangute vektori 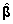korral, või

,

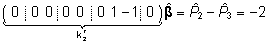mis hindab kahe- ja kolmetallelisest pesakonnast pärit tallede võõrutusmasside erinevust ja on jällegi ühene mistahes parameetrite hinnangute vektori 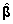korral.