Vähimruutkeskmised

Vähimruutkeskmised (VRK; inglisekeeles least square means, LSM), mis esitatakse sageli teadusartiklites ja mille hindamisvõimalust pakuvad paljud statistikaprogrammid, on oma olemuselt samuti hinnatavad parameeterfunktsioonid. Nende laialdane kasutamine on tingitud sellest, et ühelt poolt on tegu tõepoolest lihtsalt mõistetavate hinnangutega uuritava tunnuse keskmistele väärtustele faktorite tasemete alusel moodustatud gruppides, teiselt poolt on aga vähimruutkeskmiste hindamise metoodika märksa täiuslikum võrreldes tavaliste aritmeetiliste keskmiste arvutamisega -- VRK-d leitakse baseeruvana mudelil ja on korrigeeritud mudelis sisalduvate segavate faktorite mõjude ja andmestiku mittetasakaalulisuse suhtes (seetõttu erinevad vähimruutkeskmised üldjuhul tavalistest keskmistest).

Näide 11. Illustreerime vähimruutkeskmiste leidmist tallede võõrutusmassi näite varal. Üks variant mudeli (1) parameetrite hinnanguist oli esitatud vektorina (18):

.

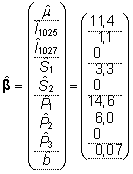Kõikvõimalikud vähimruutkeskmised koos arvutusvalemitega (ja võrdluseks ka tavalised aritmeetilised keskmised) on esitatud järgnevas tabelis.

Efekt		VRK
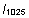	27,2
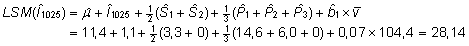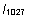	29,5
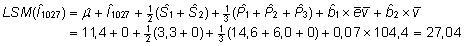S1	29,2
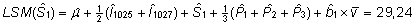S2	27,0
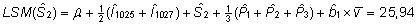P1	35,0
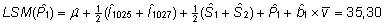P2	27,0
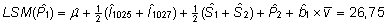P3	22,0
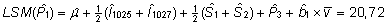