|
Juhuslike
faktorite realiseerunud väärtuste prognoosimine (BLUP)
Et
juhuslikud efektid pole konstandid, nagu fikseeritud
efektid, vaid kujutavad enesest mingist jaotusest
pärinevaid juhusliku suuruse (juhusliku faktori)
realiseerunud väärtusi, tuleb nende hindamisel
arvestada ka selle jaotuse dispersiooniga (ehk teisiti
väljendatuna, juhuslike efektide poolt määratud
osaga uuritava tunnuse koguvarieeruvusest). Mudeli
(4) korral tähendab
see dispersioonimaatriksite (8)
teadmist.
Juhul,
kui dispersioonimaatriks (8)
on teada, avaldub juhuslike faktorite realiseerunud
väärtuste vektori u parim lineaarne
nihketa prognoos (BLUP, best linear unbiased prediction)
kujul
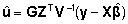 , , |
(19)
|
kus
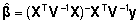 on
fikseeritud efektide üldine vähimruutude
hinnang. Seejuures tehakse siin inglisekeelses kirjanduses
selget vahet sõnadel hinnang (estimate)
ja prognoos (prediction) -- hinnatakse midagi
fikseeritut, konstantset, prognoositakse aga midagi,
mille ilmnemine sõltub juhusest. on
fikseeritud efektide üldine vähimruutude
hinnang. Seejuures tehakse siin inglisekeelses kirjanduses
selget vahet sõnadel hinnang (estimate)
ja prognoos (prediction) -- hinnatakse midagi
fikseeritut, konstantset, prognoositakse aga midagi,
mille ilmnemine sõltub juhusest.
Fikseeritud
efektide hindamine ning juhuslike efektide prognoosimine
valemite (17)
ja (19) alusel nõuab vaatluste dispersioonimaatriksi
V (8)
pöördmaatriksi leidmist, milline operatsioon
võib vähegi suurema andmestiku korral
problemaatiliseks kujuneda. Üks 20. sajandi suurimaid
segamudelite ja aretusteooria arendajaid C. Henderson
pakkus 1950. aastal välja normaalvõrrandile
(12) sarnase maatriksvõrduse, mis võimaldab
korraga leida nii BLUE(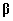 )
kui ka BLUP(u) ja seda ilma vaatluste dispersioonimaatriksit
pööramata. Tänapäeval tuntaksegi
järgnevat maatriksvõrdust Hendersoni
segamudeli võrrandina (või lihtsalt
segamudeli võrrandina, inglisekeeles mixed
model equation, MME): )
kui ka BLUP(u) ja seda ilma vaatluste dispersioonimaatriksit
pööramata. Tänapäeval tuntaksegi
järgnevat maatriksvõrdust Hendersoni
segamudeli võrrandina (või lihtsalt
segamudeli võrrandina, inglisekeeles mixed
model equation, MME):
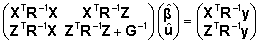 . . |
(20)
|
Traditsioonilise
segamudeli korral, kus vealiikmele ja juhuslikele
efektidele vastavad disper-sioonimaatriksid R
ja G esituvad kujul (9)
ja (10), on võrrand
(20) kirjutatav ka kujul
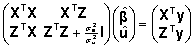 , , |
(21)
|
millest
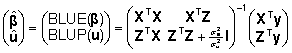 . .
Kuna
praktikas sageli dispersioonimaatrikseid võrrandis
(20) või dispersioonikomponente võrrandis
(21) teada pole, tuleb need enne efektide prognoosimist
andmetest hinnata, misjärel tehakse segamudeli
võrrandis asendused 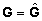 ja
ja 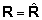 (ehk
(ehk 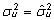 ja
ja 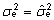 ).
On tõestatud, et juhul, kui uuritav tunnus
on sümmeetrilise jaotusega (näiteks normaaljaotusega),
on selliselt saadud fikseeritud efektide hinnangud
ning juhuslike efektide prognoosid nihketa hinnangud
BLUE( ).
On tõestatud, et juhul, kui uuritav tunnus
on sümmeetrilise jaotusega (näiteks normaaljaotusega),
on selliselt saadud fikseeritud efektide hinnangud
ning juhuslike efektide prognoosid nihketa hinnangud
BLUE(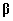 )-le
ja BLUP(u)-le. )-le
ja BLUP(u)-le.
Segamudeli
võrrandis on juhuslikele efektidele vastavad
read/veerud lineaarselt sõltumatud ega vaja
hinnangu ühesuseks erinevalt fikseeritud efektidest
lisakitsenduste rakendamist (lisakitsendused võivad
olla endiselt vajalikud fikseeritud efektide hindamisel).
Andmaks
pisut ettekujutust, mis vahe on faktori mõjude
hinnanguil sõltuvalt sellest, kas käsitleda
faktorit fikseerituna või juhuslikuna, vaatleme
lihtsaimat dispersioonanalüüsi mudelit,
mis sisaldab vaid vabaliiget 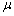 ja üht diskreetset faktorit u:
ja üht diskreetset faktorit u:
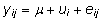 . . |
(22)
|
Käsitledes
faktorit u fikseerituna, võime parima
lineaarse nihketa hinnangu [valem (13)] faktori u
tasemele ui kirjutada kujul
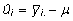 , , |
(23)
|
kus
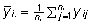 ja
ni tähistab vaatluste arvu
faktori i. tasemel -- seega on vaid üht
faktorit sisaldava dispersioonanalüüsi mudeli
korral iga faktori mõju hinnanguks temale vastavate
uuritava tunnuse väärtuste aritmeetilise
keskmise erinevus üldkeskmisest ja
ni tähistab vaatluste arvu
faktori i. tasemel -- seega on vaid üht
faktorit sisaldava dispersioonanalüüsi mudeli
korral iga faktori mõju hinnanguks temale vastavate
uuritava tunnuse väärtuste aritmeetilise
keskmise erinevus üldkeskmisest 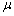 . .
Lugedes aga u juhuslikuks, avaldub tema i.
taseme mõju ui parim lineaarne
nihketa prognoos (19) seosena
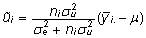 . . |
(24)
|
Valemite
(23) ja (24) võrdlemisel hakkab silma, et juhuslike
efektide hinnangud on alati väiksemad, võrreldes
fikseeritud efektide hinnangutega (sest 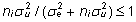 ).
Seejuures kehtib intuitiivselt mõistetav loogika
-- mida tugevam on faktori mõju, seda sarnasemad
on fikseeritud ja juhusliku mudeli eeldusel leitud
efektide hinnangud (seda suurem on dispersioonikomponendi ).
Seejuures kehtib intuitiivselt mõistetav loogika
-- mida tugevam on faktori mõju, seda sarnasemad
on fikseeritud ja juhusliku mudeli eeldusel leitud
efektide hinnangud (seda suurem on dispersioonikomponendi
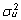 väärtus
võrreldes jääkvarieeruvusega väärtus
võrreldes jääkvarieeruvusega 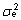 ).
Samuti nähtub valemeist (23) ja (24), et faktori
i. tasemel sooritatud mõõtmiste
arvu ni suurenedes väheneb
erinevus selle taseme mõju hinnangute ).
Samuti nähtub valemeist (23) ja (24), et faktori
i. tasemel sooritatud mõõtmiste
arvu ni suurenedes väheneb
erinevus selle taseme mõju hinnangute 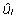 ja ja 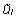 (leituna
vastavalt kas fikseeritud või juhuslikust mudelist)
vahel. (leituna
vastavalt kas fikseeritud või juhuslikust mudelist)
vahel.
Näide
12. Käsitleme nüüd mudeliga (1)
kirjeldatud tallede võõrutusmassi
näiteanalüüsis jäära mõju
juhuslikuna (andmestikus oleva kahe jäära
ja nende kokku üheksa järglase alusel
hinnatavad isa mõjud esindavad vaid juhuslikku
väljavõtet kõigist isalt järglasele
päranduda võivatest geenikomplektidest).
Mudeli fikseeritud ja juhuslikele efektidele vastavad
plaanimaatriksid on
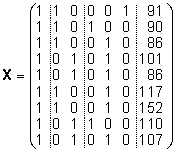 ja
ja 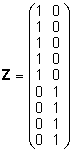
ning
hinnatavate parameetrite vektorid esituvad kujul
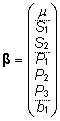 ja
ja 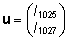 . .
Üheste
lahendite saamise huvides võrdsustame nulliga
fikseeritud faktorite viimaste tasemete mõjud
(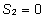 , , 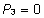 ) ning eemaldame neile vastavad veerud plaanimaatriksist
X, saades maatrikstehete läbiviimisel
kasutatava täisastakuga plaanimaatriksi ) ning eemaldame neile vastavad veerud plaanimaatriksist
X, saades maatrikstehete läbiviimisel
kasutatava täisastakuga plaanimaatriksi
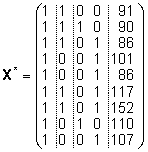 . .
Et
juhuslike efektide u ja e dispersioonimaatriksid
on diagonaalsel kujul (11), on mudeli parameetrid
hinnatavad segamudeli võrrandist (21). Viimase
rakendamiseks vajaliku dispersioonikomponentide
suhte 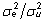 saab avaldada tallede võõrutusmassi
päritavusest h2, lugedes
viimase teadaolevaks:
saab avaldada tallede võõrutusmassi
päritavusest h2, lugedes
viimase teadaolevaks:
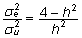 . .
Võttes
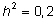 , saame , saame 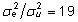 . .
Seega
avaldub segamudeli võrrandi (21) kordajate
maatriksi parem alumine nurk 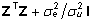 kujul
kujul
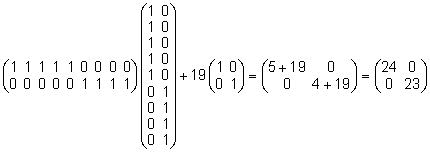
ning kogu segamudeli võrrand on peale plaanimaatriksite
korrutamistehete sooritamist järgmine:
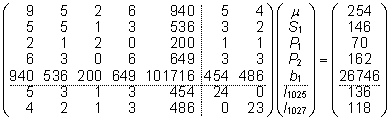 . .
Selle
võrrandi lahendina saame parameetrite hinnangute
vektori
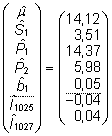 . .
Võrreldes
fikseeritud mudelist saadud hinnangutega (18)
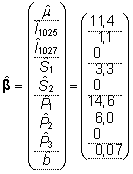
on ootuspäraselt vähenenud jääradevaheline
erinevus -- on ju jäära mõjuga
seletatav võõrutusmasside erinevus
19 korda väiksem juhusliku vea arvele jäänud
varieeruvusest (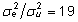 ),
mis, nagu nähtus valemeist (23) ja (24), toob
kaasa väiksemad juhuslike isamõjude
hinnangud. Loomulikult muutusid tänu mudeli
muutmisele mingil määral ka fikseeritud
efektide hinnangud, aga faktorite tasemete järjestus
jäi endiseks -- jäär-tallede võõrutusmass
on suurem; suurima võõrutusmassiga
on üksiktalled, seejärel kaksik- ja kolmiktalled;
võõrutusvanuse kasvades suureneb ka
tallede võõrutusmass. ),
mis, nagu nähtus valemeist (23) ja (24), toob
kaasa väiksemad juhuslike isamõjude
hinnangud. Loomulikult muutusid tänu mudeli
muutmisele mingil määral ka fikseeritud
efektide hinnangud, aga faktorite tasemete järjestus
jäi endiseks -- jäär-tallede võõrutusmass
on suurem; suurima võõrutusmassiga
on üksiktalled, seejärel kaksik- ja kolmiktalled;
võõrutusvanuse kasvades suureneb ka
tallede võõrutusmass.
Eelnevas
näites rakendatud mudelit, kus uuritava tunnuse
geneetilist determineeritust väljendava juhusliku
faktorina käsitletakse isa ning ülejäänud
faktorid on fikseeritud ja kirjeldavad mitte aditiivgeneetilisi
mõjusid, nimetatakse põllumajandusloomade
aretuses isa mudeliks (inglise keeles sire
model). Lähemalt isa mudelist ja ka teistest
segamudeli rakendustest geneetiliste parameetrite
hindamisel teistes
õppematerjalides.
|