Vaatluste keskväärtused ja kovariatsioonistruktuur fikseeritud mudeli korral

Igas lineaarses mudelis on vähemalt kaks juhuslikku liiget (mis eeldatakse traditsiooniliselt käituvat vastavalt normaaljaotuse seaduspäradele)

• uuritav tunnus, kui populatsioonist juhuslikult valitud indiviididel sooritatud mõõtmiste tulemusi koondav suurus, ja
   
• juhuslik viga.

Juhul, kui mudel sisaldab faktoritena üksnes fikseeritud mõjusid, on need kaks ka mudeli ainsad mittekonstantsed ja seega mittenullilist dispersiooni omavad suurused.

On loomulik eeldada, et juhuslike vigade keskväärtus võrdub nulliga (mudeli keskmine viga on nul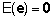l): . Uuritava tunnuse keskväärtus avaldub fikseeritud mudeli (2) korral kujul

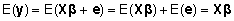
ja dispersioonimaatriks võrdusena

.

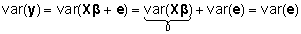(6)