|
Üldine
lineaarne mudel maatrikskujul
Üldiste
lineaarsete mudelite maatrikskujul esitamiseks kasutatakse
eriliste maatriksite abi, mis seostavad iga objekti
just temal sooritatud mõõtmistega või
temale vastava faktori tasemega. Selliseid maatrikseid,
mille ridade arv võrdub uuritud objektide arvuga
ja veergude arv mudelist hinnatavate efektide arvuga,
nimetatakse plaani- e disainimaatriksiteks.
Regressioonivõrrand,
kirjapanduna objekti i kohta,
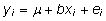 , ,
näeb
maatrikskujul esitatuna välja järgmiselt:
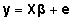 , , |
(2)
|
kus
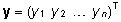 ja
ja 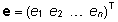 on vastavalt funktsioontunnuse väärtuste
ja prognoosivigade vektorid,
on vastavalt funktsioontunnuse väärtuste
ja prognoosivigade vektorid, 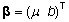 on hinnatavate parameetrite vektor ja plaanimaatriks
on hinnatavate parameetrite vektor ja plaanimaatriks
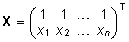 sisaldab ühte veergu kummagi hinnatava parameetri
tarvis - esimene, ühtedest koosnev veerg tähendab,
et kõigil objektidel mõõdetud
uuritava tunnuse väärtusi püütakse
prognoosida sama keskmise
sisaldab ühte veergu kummagi hinnatava parameetri
tarvis - esimene, ühtedest koosnev veerg tähendab,
et kõigil objektidel mõõdetud
uuritava tunnuse väärtusi püütakse
prognoosida sama keskmise 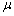 abil, teine, argumenttunnuse väärtusi sisaldav
veerg seob igal objektil mõõdetud uuritava
tunnuse väärtuse läbi kordaja b
just temale vastava argumenttunnuse väärtusega.
abil, teine, argumenttunnuse väärtusi sisaldav
veerg seob igal objektil mõõdetud uuritava
tunnuse väärtuse läbi kordaja b
just temale vastava argumenttunnuse väärtusega.
Dispersioonanalüüsi
korral koosneb plaanimaatriks vaid nullidest ja ühtedest
- mingile objektile vastavas reas ja faktori tasemele
vastavas veerus on 1, kui mõõtmine antud
objektil on sooritatud just sellel tasemel, ja 0 vastupidisel
juhul.
Näiteks ühefaktorilise dispersioonanalüüsi
mudel
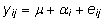
on
maatriksite abil esitatav kujul
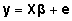
ehk
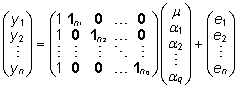 . .
Siin
ni tähistab faktori i-ndale
tasemele vastavate objektide arvu, q on faktori
tasemete arv (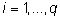 ), ),
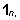 on
ühtedest koosnev on
ühtedest koosnev 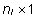 -vektor: -vektor:
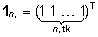 , ja 0
on sobiva dimensiooniga nullidest koosnev vektor. , ja 0
on sobiva dimensiooniga nullidest koosnev vektor.
Kovariatsioonanalüüsi
mudel, milles on nii mittearvulisi kui ka arvulisi
faktortunnuseid, sisaldab plaanimaatriksis nii nulle
ja ühtesid sisaldavaid veerge kui ka pidevate
argumenttunnuste väärtuseid.
Kokkuvõttes
kujutab üldise lineaarse mudeli maatriksesitus
enesest tavalise lineaarvõrranditesüsteemi
maatriksesitust, kus kordajate maatriksi rollis on
plaanimaatriks, tundmatud parameetrid on koondatud
vektorisse 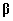 ja vabaliikmete veerg moodustub vahest
ja vabaliikmete veerg moodustub vahest 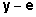 . .
Näide
3. Paneme näite
2 mudeli (1) kirja ka maatrikskujul (2).
Vektor
y on tallede võõrutusmasside
vektor kujul
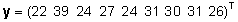 . .
Plaanimaatriks
X sisaldab ühte rida iga vaatluse ja
ühte veergu iga vektoris 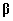 kirjas oleva mudeli parameetri kohta.
kirjas oleva mudeli parameetri kohta.
Hinnatavate
parameetrite vektor 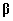 sisaldab üheksat elementi (parameetrite tähistused
on üle võetud sama mudeli objektiviisi
esitusest):
sisaldab üheksat elementi (parameetrite tähistused
on üle võetud sama mudeli objektiviisi
esitusest):
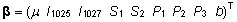 . .
Plaanimaatriks
X, mis seob iga vaatluse just temale vastava
faktori tasemega või väärtusega,
näeb praeguse tallede järjestuse korral
välja järgmine:
 , , |
(3)
|
(parema
jälgitavuse huvides on erinevatele faktoritele
vastavad blokid eraldatud punktiirjoontega).
Juhuslike
vigade vektor on kujul
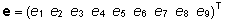 . .
Näitamaks,
et eelnevalt defineeritud plaanimaatriks tõepoolest
iga talle võõrutusmassi just temale
vastavate faktorite tasemetega seob, asendame kõik
väljakirjutatud vektorid ja maatriksid mudelisse
(2) ning sooritame korrutustehte X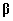 .
Tulemuseks saame maatriksvõrduse .
Tulemuseks saame maatriksvõrduse
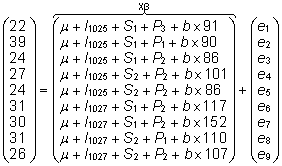 . .
|