Mudeli esitus objektiviisi

Mudeli objektiviisi esitamisel avaldatakse igal objektil mõõdetud väärtus üldkeskmise (nn vabaliikme, inglise keeles intercept), objektile vastavate mõjude ja konkreetse objekti omapära e faktoritega kirjeldamata jääva osa (mudeli vea) summana.

Erinevate objektide ja faktorite tasemete üheseks identifitseerimiseks kasutatakse indeksite abi: igale diskreetsele faktorile omistatakse põhiindeks (harilikult i, j, k, l, …), mis näitab iga objekti kohta just temale omase faktori taseme mõju, peale selle tähistab üks lisaindeks objekti (mõõtmist) ennast. Faktorite koosmõjude korral kirjutatakse indeksiks mõlema faktori indeksid, allutatud faktorite puhul tuuakse tavaliselt faktori enese põhiindeksi järel sulgudes ära kõigi nende faktorite indeksid, millele antud faktor allub. Pideva faktori tähis omab kogu indeksite komplekti, sest märgib konkreetsel objektil ja diskreetsete faktorite kombinatsioonil sooritatud mõõtmise tulemust, mille mõju samal objektil ja diskreetsete faktorite kombinatsioonil mõõdetud uuritava tunnuse väärtusega väljendab vastav regressioonikordaja.

Näide 2. Uuritavaks tunnuseks on tallede võõrutusmass ja analüüsi eesmärgiks on võrrelda ühes lambafarmis kasutatud kahte isa. Objektiivsemate tulemuste huvides soovitakse arvestada ka talle soo ja pesakonna suuruse kui diskreetsete faktorite ning võõrutusvanuse kui pideva faktori mõjudega. Andmed on kirjas järgnevas tabelis.

Sugu	Psk suurus	Võõrutusmass	Võõrutusvanus	Isa
1	3	22	91	1025
1	1	39	90	1025
1	2	24	86	1025
2	2	27	101	1025
2	2	24	86	1025
1	2	31	117	1027
1	2	30	152	1027
2	1	31	110	1027
2	2	26	107	1027

Üldise lineaarse mudeli võib toodud ülesande püstituse korral esitada järgmiselt:

,

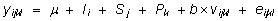(1)

kus parameetrit 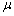võib mõista kui nö keskmist tallede 100 päeva kehamassi (mis siiski ei pruugi võrduda aritmeetilise keskmisega, sest on tegelikult faktorite keskmine mõju);
y_ijkl tähistab objektil l sooritatud mõõtmist e antud juhul l. talle 100 päeva kehamassi (ülejäänud indeksid fikseerivad täpselt ära vaatlusaluse talle isa, sünniaasta jne), ;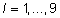
I_i tähistab isa i mõju, 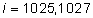(või siis i = 1, 2);
S_j märgib soo j mõju, ;
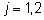P_k on pesakonna suuruse k mõju, ;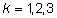
v_ijkl tähistab konkreetse talle võõrutusvanust ja b on võõrutusmassi lineaarset sõltuvust võõrutusvanusest iseloomustav regressioonikordaja;
e_ijkl on talle l omapära (e juhuslik viga).