|
Dispersioonikomponentide hindamine -> Dispersioonanalüüsi
meetod (ANOVA-meetod)
Nii
fikseeritud efektide hindamine üldistatud vähimruutude
meetodil (17),
juhuslike efektide parim lineaarne nihketa prognoos
(19) kui ka Hendersoni
segamudeli võrrandi (20)
või (21)
lahendamine eeldab dispersioonikomponentide kaudu
defineeritud dispersioonimaatriksite teadmist. Nagu
nähtus eelneva peatüki näitest, piisab
sageli ka dispersioonikomponentide suhte või
mõne populatsiooni geneetilise parameetri väärtuse
teadmisest. Samas aga ei ole meil kuidagi võimalik
teada dispersioonikomponentide suhet kõigi
ette tulla võivate tunnuste või mudelite
korral ning ka meie poolt analüüsitava populatsiooni
geneetiline struktuur ei pruugi vastata teadaolevate
geneetiliste parameetritega kirjeldatud populatsioonile.
Valede dispersiooniparameetrite kasutamisega kaasnevad
aga ka valed mõjuhinnangud, aretusväärtused
ja seeläbi ka valed otsused tuleviku strateegiate
osas.
Dispersioonikomponentide
hindamiseks on välja töötatud hulk
erinevaid meetodeid. Nende mitmesus on tingitud sellest,
et vähegi keerulisema mudeli puhul ei ole võimalik
välja kirjutada dispersioonikomponentide parimate
omadustega analüütilisi lahendeid, kasutada
tuleb kas teatud lihtsustavaid eeldusi või
siis ligilähedasi matemaatilisi arvutusmeetodeid.
Meetodite matemaatiline keerukus on ka põhjuseks,
miks üldiste lineaarsete segamudelite rakenduste
tudeerimisel dispersioonikomponentide hindamine kõrvale
jäetakse. Samas baseerub peamiste populatsioonigeneetiliste
parameetrite, nagu päritavuskoefitsient, korduvus
ja geneetilised korrelatsioonikordajad, hindamine
enamasti just dispersioonikomponentide hindamisel.
Andmete
tasakaalulisuse (vt pt
2.4) ja vaatluste sõltumatuse eeldusel
on dispersioonikomponentide hinnangud leitavad järgnevalt
tutvustatava metoodika kohaselt tavalisest dispersioonanalüüsist.
Mittetasakaalulise andmestiku ja keerulisema kovariatsioonistruktuuri
korral on kõige universaalsemaks osutunud järgmise
punktis tutvustatav REML-meetod.
Dispersioonanalüüsi meetodi (ANOVA-meetodi)
selgitamiseks võtame vaatluse alla ühefaktorilise
dispersioonanalüüsi mudeli (22):
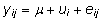 . .
Eeldame
et faktor u on juhuslik ning et efektid ui
ja eij on sõltumatud ja normaaljaotusega.
Samuti eeldame, et faktoril u on a taset,
igal tasemel on sooritatud täpselt n mõõtmist
ning kokku on mõõtmisi 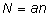 .
Dispersioonanalüüsi arvutused koondatakse
nn dispersioonanalüüsi tabelisse, mis vaatlusaluse
mudeli tarvis on toodud tabelis 1. .
Dispersioonanalüüsi arvutused koondatakse
nn dispersioonanalüüsi tabelisse, mis vaatlusaluse
mudeli tarvis on toodud tabelis 1.
Tabel
1. Dispersioonanalüüsi tabel mudeli
(22) korral.
|
Varieeruvuse
allikas
|
Ruutude
summa *
|
Vabadusastmete
arv
|
Keskruut
|
Keskruudu
ooteväärtus
|
| Faktor
u |
|
|
|
|
| Jääk |
|
|
|
|
*
siin 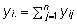 ja
ja 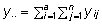 . .
ANOVA-hinnangud
dispersioonikomponentidele 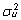 ja
ja 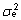 saadakse, võrdsustades keskruudud nende ooteväärtustega:
saadakse, võrdsustades keskruudud nende ooteväärtustega:
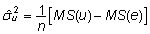
ja
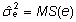 . .
Mittetasakaaluliste
andmete ja ühefaktorilise dispersioonanalüüsi
mudeli (22) korral on juhusliku faktori poolt määratud
osa uuritava tunnuse varieeruvusest, 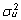 ,
ANOVA-meetodil hinnatav valemist ,
ANOVA-meetodil hinnatav valemist
 , ,
kus
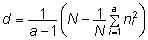 ja
ni tähistab mõõtmiste
arvu faktori u tasemel i (näiteks
on tegu i. isa järglaste arvuga). ja
ni tähistab mõõtmiste
arvu faktori u tasemel i (näiteks
on tegu i. isa järglaste arvuga).
|