Kovariatsioonistruktuur

Traditsioonilisel üldiste lineaarsete mudelite analüüsil (nagu näiteks ka tavalise regressioon- ja dispersioonanalüüsi korral) eeldatakse dispersioonimaatriksite diagonaalset kuju. Segamudelite tarvis on selline lihtne kovariatsioonistruktuur defineeritud seostega (9) ja (10). Et aga tegelikkus (uuritava(te) tunnus(t)e varieeruvus) sageli nii triviaalselt kirjeldatav pole, leiab reaalsete andmete analüüsil kasutust suur hulk rohkem või vähem keerukaid dispersioonistruktuure, mis on faktorite mõjude ja juhuslike vigade sõltumatuse eeldusel kokkuvõtvalt esitatavad dispersioonimaatriksina (8).

Fikseeritud mudelite puhul on levinuimad kõiksugu korduvate mõõtmiste analüüsi mudelid, kus püütakse arvesse võtta ühel ja samal objektil sooritatud mõõtmistele vastavate mudeli jääkide korrelleeritust.

Näide 6. Olgu meil uuritavaiks objektideks eesti maatõugu lehmad, kellel kõigil on fikseeritud esimese kolme laktatsiooni piimatoodangud. Järgnevalt on esitatud väljavõte andmetabelist.

ID	Lakt. nr.	Piim
3396	1	4119
3396	2	5857
3396	3	6260
3990	1	3106
3990	2	3934
3990	3	5171
4390	1	2473
4390	2	3301
4390	3	2958
...	...	...

Ükskõik, milliste faktortunnuste mõju me ka uurida tahame, on loomulik eeldada, et sama lehma piimatoodangud ei ole sõltumatud. 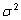Mudelisse saab viimase kirja panna jääkdispersioonimaatriksi R struktuuri abil, kus endiselt vastab kõigile vaatlustele juhuslike vigade dispersioon , aga lisaks võib defineerida (ja lasta arvutil ka andmetest hinnata) samale loomale vastavate mudeli jääkliikmete koosvarieeruvust peegeldava dispersioonikomponendi , misjärel jääkdispersioonimaatriks esitub kompaundsümmeetrilisel kujul

.

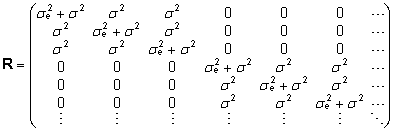Sammu võrra keerulisema dispersioonistruktuuri saame, kui eeldame, et mida suurem on mõõtmiste ajaline vahe, seda nõrgem on nende vaheline seos, ehk antud näite puhul: 1. ja 2. laktatsiooni toodangud on omavahel tugevamini seotud, kui 1. ja 3. laktatsiooni toodangud. Üks võimalus seda mudelisse kirja panna on kasutada jääkdispersioonimaatriksi defineerimisel esimest järku autoregressiivset struktuuri kujul

,

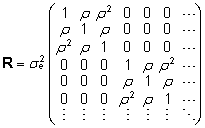kus parameetri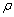t võib mõista kui ühe ja sama looma järjestikuste vaatluste vahelist autokorrelatsioonikordajat, .

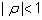Segamudelite puhul tuleb arvestada ka juhuslike faktorite mõjude võimaliku korreleeritusega, mis tähendab dispersioonimaatriksi G struktuuri erinevust traditsioonilisest diagonaalsest kujust (10). Loomade aretuses väljendub see enamasti kõikvõimalike sugulussidemete matemaatilisel kujul väljendamises ja mudelisse kaasamises -- taolisel kovariatsioonistruktuuri defineerimisel põhineb näiteks aretusväärtuste prognoosimine looma mudelist.