|
Vähimruutude
hinnangud
Faktorite
mõjud mudelist 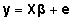 (2) hinnatakse vähimruutude meetodil, st et parameetervektori
(2) hinnatakse vähimruutude meetodil, st et parameetervektori
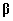 hinnang hinnang
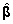 valitakse
selliselt, et mudeli vigade ruudud oleks minimaalsed.
Maatrikskujul on vähimruutude tingimus mudeli
(2) tarvis väljendatav seosena valitakse
selliselt, et mudeli vigade ruudud oleks minimaalsed.
Maatrikskujul on vähimruutude tingimus mudeli
(2) tarvis väljendatav seosena
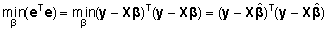 . .
Hinnangu
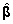 avaldamiseks
tuleb mudeli (2) vigade ruutude summast avaldamiseks
tuleb mudeli (2) vigade ruutude summast
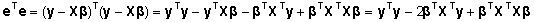
võtta
tuletis 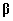 järgi ja võrdsustada tulemus nulliga.
Diferentseerimise tagajärjel saame
järgi ja võrdsustada tulemus nulliga.
Diferentseerimise tagajärjel saame
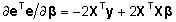
ning
viimase avaldise nulliga võrdsustamisest järeldub,
et
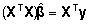 , , |
(12)
|
millest
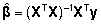 . . |
(13)
|
Võrrand
(12) on tuntud kui normaalvõrrand (normal
equation) ja hinnang (13) kujutab enesest parameetervektori
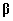 vähimruutude
hinnangut (OLS, ordinary least squares),
mis diagonaalse võrdsete dispersioonikomponentidega
jääkdispersioonimaatriksi (9) korral on
parim lineaarne nihketa hinnang (BLUE,
best linear unbiased estimator). Sõna
"parim" hinnangu nimetuses tähendab,
et tegu on täpseima e väikseima dispersiooniga vähimruutude
hinnangut (OLS, ordinary least squares),
mis diagonaalse võrdsete dispersioonikomponentidega
jääkdispersioonimaatriksi (9) korral on
parim lineaarne nihketa hinnang (BLUE,
best linear unbiased estimator). Sõna
"parim" hinnangu nimetuses tähendab,
et tegu on täpseima e väikseima dispersiooniga
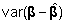 hinnanguga
(efektiivse hinnanguga) ning sõna "nihketa"
märgib hinnangu nn keskmist õigsust (süstemaatilise
vea puudumist). hinnanguga
(efektiivse hinnanguga) ning sõna "nihketa"
märgib hinnangu nn keskmist õigsust (süstemaatilise
vea puudumist).
Kui
meil on aga tegu keerulisema kovariatsioonistruktuuriga,
kus 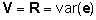 ei ole võrdsete dispersioonikomponentidega
diagonaalmaatriks, siis pole ka valemiga (13) defineeritud
hinnang enam BLUE parameetervektorile
ei ole võrdsete dispersioonikomponentidega
diagonaalmaatriks, siis pole ka valemiga (13) defineeritud
hinnang enam BLUE parameetervektorile 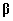 .
Hädast aitab välja kaval teisendus. Nimelt,
kui teame dispersioonimaatriksit V, mis tänu
dispersiooni definitsioonile on alati positiivselt
määratud ja mistõttu leiduvad ka .
Hädast aitab välja kaval teisendus. Nimelt,
kui teame dispersioonimaatriksit V, mis tänu
dispersiooni definitsioonile on alati positiivselt
määratud ja mistõttu leiduvad ka
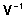 ja
selline maatriks ja
selline maatriks 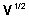 ,
et ,
et 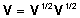 ,
võime võrrandi (2) mõlemaid pooli
vasakult korrutada maatriksiga ,
võime võrrandi (2) mõlemaid pooli
vasakult korrutada maatriksiga 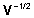 ,
saades tulemuseks mudeli ,
saades tulemuseks mudeli
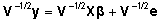 . .
Tähistades
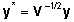 , ,
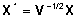 ja ja
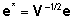 saame
viimase mudeli esitada võrrandina saame
viimase mudeli esitada võrrandina
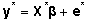 , , |
(14)
|
kusjuures
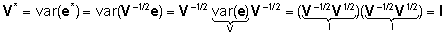 . .
Et
nüüd on meil dispersioonimaatriks 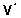 diagonaalsel kujul, nagu on vaja BLUE esitamiseks
valemi (13) abil, rakendame viimast mudelile (14)
ja saame parameetervektori hinnangu kujul
diagonaalsel kujul, nagu on vaja BLUE esitamiseks
valemi (13) abil, rakendame viimast mudelile (14)
ja saame parameetervektori hinnangu kujul
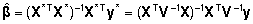 . . |
(15)
|
Viimast
hinnangut nimetatakse üldistatud vähimruutude
hinnanguks (GLS, generalized least squares).
Juhul,
kui analüüsitav mudel ei ole täisastakuga,
ei ole normaalvõrrandi kordajate maatriksid
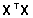 ja ja
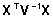 (vastavalt
tavalise ja üldistatud vähimruutude hinnangu
puhul) pööratavad ja kasutada tuleb üldistatud
pöördmaatrikseid. (vastavalt
tavalise ja üldistatud vähimruutude hinnangu
puhul) pööratavad ja kasutada tuleb üldistatud
pöördmaatrikseid.
Vähimruutude
hinnangud (13) ja (15) saavad siis üldisemad
kujud
ja
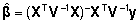 . . |
(17)
|
Näide
9. Vaatleme edasi tallede võõrutusmassi
andmestikku ja hindame talle isa, soo, pesakonna
suuruse ning võõrutusvanuse kui fikseeritud
faktorite mõjud. Garanteerimaks hinnangute
ühesust, võrdsustame nulliga iga faktori
viimase taseme efekti (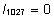 , ,
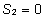 , ,
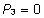 ).
Ülejäänud efektide hindamiseks paneme
kirja täisastakuga (ilma nulliga võrdsustatud
efektidele vastavate veergudeta) plaanimaatriksi ).
Ülejäänud efektide hindamiseks paneme
kirja täisastakuga (ilma nulliga võrdsustatud
efektidele vastavate veergudeta) plaanimaatriksi
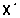 : :
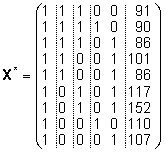 . .
Et
vaatluste dispersioonimaatriks on diagonaalsel kujul,
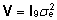 ,
ja plaanimaatriks ,
ja plaanimaatriks 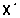 on täisveeruastakuga, saame faktorite mõjude
vektori
on täisveeruastakuga, saame faktorite mõjude
vektori
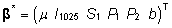
hindamiseks
kasutada valemit (13):
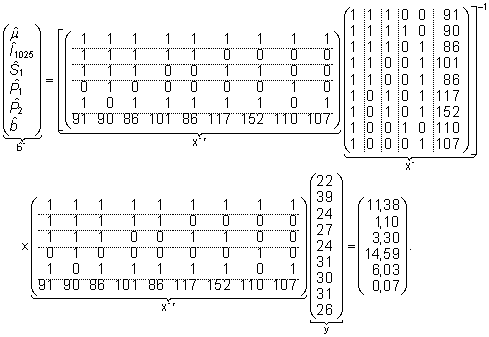
Peale
kitsenduste lisamist saame mudeli (1) parameetrite
hinnangud kujul
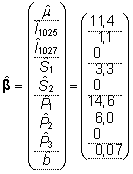 . . |
(18)
|
Võrreldes
faktorite tasemete kaupa leitud aritmeetiliste keskmistega
(vt tabelit näite lõpus) hakkab silma
jäärade paremusjärjestuse muutus
-- kui järglaste keskmiste väärtuste
alusel võinuks eelistada jäära
numbriga 1027, siis peale teiste faktorite mõjude
arvesse võtmist on ilmselge hoopis jäära
nr 1025 paremus. Andmetabelist (pt
3.1) põhjust otsides hakkab eelkõige
silma, et jäära nr 1027 järglased
on võõrutatud hiljem ja saanud seega
kauem aega kasvada (positiivset seost võõrutus-vanuse
ja võõrutusmassi vahel näitab
ka regressioonikordaja positiivne väärtus,
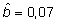 ).
Jäärade mõjude hindamine mudeli
(1) abil võimaldab nende seostega arvestada. ).
Jäärade mõjude hindamine mudeli
(1) abil võimaldab nende seostega arvestada.
Faktorite
tasemed ja neile vastavad keskmised võõrutusmassid:
|
|
|
|
|
| Pesakonna
suurus |
| 1 |
35,0 |
| 2 |
27,0 |
| 3 |
22,0 |
|
|