Üldistatud pöördmaatriks

Maatriksi A üldistatud pöördmaatriksiks nimetatakse maatriksi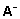t , mis rahuldab võrdust

.

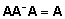Üldistatud pöördmaatriks ei ole ühene ja võib olla leitud mitmel erineval viisil.

Lihtsaim viis maatriksi A üldistatud pöördmaatriksi 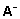leidmiseks on

• võtta maatriksist A välja maksimaalne lineaarselt sõltumatu alammaatriks (miinor) B,
• leida selle pöördmaatriks B^-1,
• asendada maatriksis A miinor B tema pöördmaatriksiga B^-1 ning kõik ülejäänud elemendid nullidega.

Näide. Eelmise punkti näites toodud maatriksi 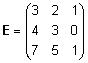 maksimaalne lineaarselt sõltumatu miinor on .

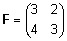Selle pöördmaatriks on 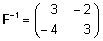ning maatriksi E üldistatud pöördmaatriks 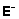esitub kujul .

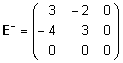Kontrollige ise, et leitud maatriks rahuldab üldistatud pöördmaatriksi tingimust (EE^-E = E)!