|
Transponeerimine,
ortogonaalsed ja idempotentsed maatriksid
Maatriksi A transponeeritud
maatriks, mida tähistatakse tavaliselt A' või
AT, saadakse, vahetades esialgse maatriksi
read ja veerud, s.t. kui B = AT,
siis bji = aij.
Näide. 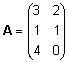 ; ;
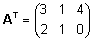 . .
Omadused
- Kui A on sümmeetriline,
siis A = AT.
- (A + B)T=AT
+ BT.
- (AB)T
= BTAT.
Maatriksit nimetatakse
idempotentseks, kui tema korrutis iseendaga
annab tulemuseks iseenda, s.t. maatriks A on
idempotentne, kui
AA
= A.
Vaid ruutmaatriks saab
olla idempotentne.
Ortogonaalne maatriks
on ruutmaatriks, mille korrutis oma transponeeritud
maatriksiga võrdub ühikmaatriksiga - maatriks U
on ortogonaalne, kui
UUT
= UTU = I.
|