| |
|
|
| 1.
Definitsioonid |
|
|
| 2.
Maatriksoperatsioonid |
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
| ¤
|
|
|
| 3.
Maatrikstehted MS Excelis |
|
|
| 4.
Enesekontroll |
|
|
| Lisa |
| ¤
|
Kogu
materjal ühe pdf-failina:
|
|
|
|
Ülesannete
lahendused
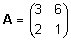 , ,
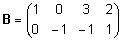 .
Näidake, et .
Näidake, et 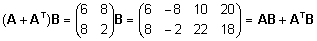 . .
Lahendus.
Standardsed maatrikstehted. Vastus on antud ülesande
tekstis.
- Näidake,
et
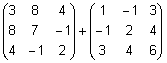 on sümmeetriline.
on sümmeetriline.
Lahendus.
Tegelikult on see, et tulemusmaatriks on sümmeetriline,
näha juba liidetavatest: mõlemad liidetavad
on sümmeetrilised maatriksid ...
- Näidake,
et suvalise pxq-maatriksi H
korral korrutismaatriksid HHT
ja HTH on sümmeetrilised.
Lahendus.
Kui maatriks H on pxq-maatriks,
siis tema transponeeritud maatriks HT
on qxp-maatriks, kusjuures 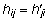 ,
kus hij on maatriksi H
i. reas ja j. veerus paiknev element
ning h'ij on maatriksi
HT j. reas ja i.
veerus paiknev element. ,
kus hij on maatriksi H
i. reas ja j. veerus paiknev element
ning h'ij on maatriksi
HT j. reas ja i.
veerus paiknev element.
Korrutismaatriksi
X = HHT i. reas
ja j. veerus paiknev element xij
avaldub kujul 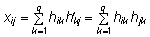
ning
j. reas ja i. veerus paiknev element
xji kujul 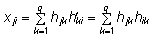 .
.
Seega
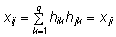 ,
iga i ja j korral. Et viimane tulemus
on sümmeetrilise maatriksi tunnus, peabki
korrutismaatriks X = HHT
olema sümmeetriline. ,
iga i ja j korral. Et viimane tulemus
on sümmeetrilise maatriksi tunnus, peabki
korrutismaatriks X = HHT
olema sümmeetriline.
Analoogselt
on näidatav ka korrutismaatriksi Y
= HTH sümmeetrilisus.
- Kontrollige,
kas
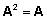 ,
kui ,
kui 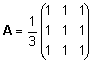 . .
Lahendus.
Tavaline maatriksite korrutamine, tingimus tulemuse
õigsuse kontrollimiseks on kirjas ülesande
tekstis (A2 = A).
- Näidake,
et
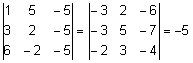 . .
Lahendus.
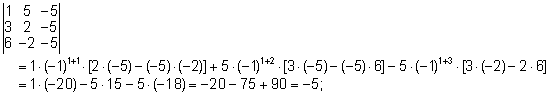
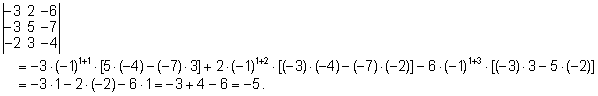
- Näidake,
et 2x2-maatriksi
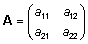 korral
korral 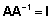 . .
Lahendus.
2x2-maatriksi A korral 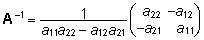 . .
Seega
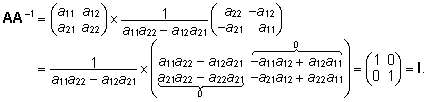
- Kas
leidub pöördmaatriks (XTX)-1,
kui
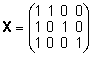 . .
Lahendus.
Ei leidu, sest maatriksi X veerud on lineaarselt
sõltuvad (esimene veerg avaldub teise,
kolmanda ja neljanda veeru summana).
Muidugi
võib teostada ka maatrikstehte XTX
ja leida tulemuseks saadud maatriksi determinandi.
Viimase 0-ga võrdumisest järeldubki
pöördmaatriksi mitteleidumine.
- Järgnevas
tabelis on toodud viie pulli tütarde 1. laktatsiooni
keskmiste näitajate erinevused populatsiooni
keskmisest.
| |
Piim,
kg
|
Välimiku
üldhinne
|
Seemenduste
arv
|
Surnult
sündide arv
|
| Pull
1 |
+2117
|
+1,5
|
+1,7
|
+0,21
|
| Pull
2 |
-985
|
+0,0
|
+0,7
|
-0,13
|
| Pull
3 |
+1421
|
+0,4
|
+0,2
|
+0,04
|
| Pull
4 |
-97
|
-1,2
|
-2,1
|
+0,05
|
| Pull
5 |
+1875
|
+0,2
|
-0,6
|
-0,07
|
Pulli
järglaste paremus või halvemus võrreldes
populatsiooni keskmisega väljendab pulli poolt
järglastele pärandatavate geenide mõju.
See, kui palju ühe ühikuline erinevus
mingi tunnuse osas rahaliselt väärt on,
et kirjas järgnevas tabelis.
|
Piim,
kg
|
Välimiku
üldhinne
|
Seemenduste
arv
|
Surnult
sündide arv
|
|
3.-
EEK
|
150.-
EEK
|
-250.-
EEK
|
-1500.-
EEK
|
Millise
maatrikstehtega saab kahe toodud tabeli (maatriksi)
alusel leida korraga iga pulli poolt järglastele
pärandatavate geenide (so sisuliselt spermadoosi)
rahalist väärtust?
Leidke vastav väärtus iga pulli tarvis
ja järjestage pullid.
Lahendus.
Moodustame tabelis toodud pullide tütarde keskmiste
näitajate ja populatsiooni keskmiste näitajate
vahelistest erinevustest maatriksi P (igale
pullile vastab maatriksis üks rida ja igale
näitajale üks veerg) ning näitajate
rahalistest väärtustest veeruvektori x:
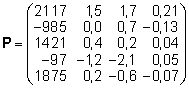 , ,
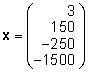 . .
Pullide
poolt järglastele pärandatavate geenide
rahalised väärtused on siis esitatavad
maatrikskorrutise Px tulemuseks oleva vektori
kujul:
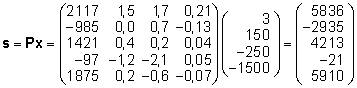 . .
Seega
on pullide järjestus järgmine: Pull5,
Pull1, Pull3, Pull4, Pull2. Seejuures pärandavad
pullid 5, 1 ja 3 järglastele geneetilise potentsiaali
tuua omanikele populatsiooni keskisega võrreldes
enam kasu ning pullid 2 ja 4 pärandavad järglastele
geneetilise potentsiaali tuua omanikele populatsiooni
keskisega võrreldes vähem kasu.
- Leidke
üldist maatriksfunktsioonide algoritmi kasutades,
millega võrdub M(M-2
+ M-1M), kus maatriks M
on kujul
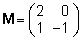 . .
Lahendus.
Leiame esmalt maatriksi M omaväärtused,
lahendades järgmise võrrandi:
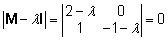 =>
=> 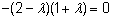 =>
=> 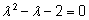 =>
=> 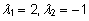 . .
Konstantsete
maatriksite Z1 ja Z2
leidmiseks tuleb konstrueerida vajalik võrrandisüsteem
ja see lahendada:
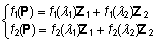 =>
=> 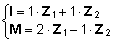 =>
=> 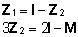 =>
=> 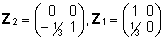 . .
Edasi
saabki arvutada M(M-2
+ M-1M):
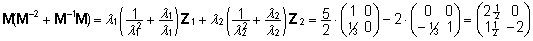 . .
- Teostage
eelmises ülesandes toodud tehe ühe tehetejärjekorrana
MS Excelis.
Lahendus.
Paiknegu maatriks M Exceli töölehel
lahtrites B2:C3. Tehte M(M-2
+ M-1M) tulemusmaatriks
on siis leitav tehetejärjekorraga
=MMULT(B2:C3;(MMULT(MINVERSE(B2:C3);MINVERSE(B2:C3))+MMULT(MINVERSE(B2:C3);B2:C3)))

|
|
| <
Eelmine |
|
|