Determinant

.

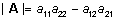Vahel tähistatakse determinanti ka det(A).

Enam kui kahedimensionaalse ruutmaatriksi determinant on leitav valemist

,

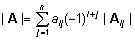kus i tähistab maatriksi A i-ndat rida ja A_ij on maatriksi A alammaatriks, mis on saadud esialgsest maatriksist i. rea ja j. veeru ärajätmise tulemusena. Sellist alammaatriksit nimetatakse miinoriks.

Maatriksit nimetatakse singulaarseks, kui tema determinant võrdub nulliga ja mittesingulaarseks, kui tema determinant on nullist suurem.

Omadused

1. |A| = |A^T|.
2. Kui maatriksid A ja B on sama järku ruutmaatriksid, siis |AB| = |A||B|.
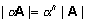3. , A on nxn-maatriks ja 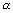suvaline skalaar.
4. |I_n| = 1.
5. Kui maatriks sisaldab kahte või enamat võrdset rida või veergu, siis tema determinant võrdub nulliga.
6. Diagonaalmaatriksi determinant võrdub tema diagonaalielementide korrutisega, s.t. kui 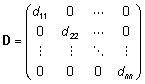, siis .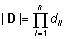

Näide. .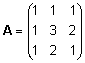
Võttes i = 1, s.t. kasutades arvutamisel maatriksi A esimese rea elemente ja nendele vastavaid miinoreid, avaldub determinant kujul

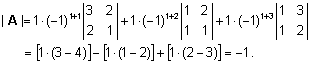
Sama tulemuse saaksime ka teisi ridasid (s.t. i = 2 või 3) aluseks võttes, samuti kasutades rea asemel veergu ja sellele vastavaid miinoreid.