|
Üldine
maatriksfunktsioonide leidmise algoritm
Olgu
maatriks A ruutmaatriks. Mingi maatriksfunktsioon
f(A) on kõige üldisemalt
esitatav kujul
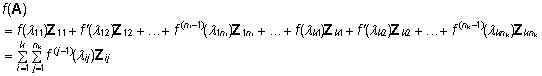 , ,
kus
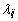 on maatriksi A i. omaväärtus
ja indeks j märgib selle kordsust,
on maatriksi A i. omaväärtus
ja indeks j märgib selle kordsust, 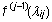 on
funktsiooni f (j-1). tuletise väärtus
kohal on
funktsiooni f (j-1). tuletise väärtus
kohal 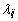 ning Zij on üksnes maatriksist
A (ja mitte funktsioonist f) sõltuv
konstantne maatriks.
ning Zij on üksnes maatriksist
A (ja mitte funktsioonist f) sõltuv
konstantne maatriks.
Maatriksi
A omaväärtused leitakse võrrandist
ja konstantsete maatriksite Zij
leidmiseks konstrueeritakse võimalikult lihtsatest
maatriksi A funktsioonidest (a'la ühikteisendus
f(A) = I, samasusteisendus f(A)
= A, ruutteisendus f(A) = A2
jne) võrrandisüsteem ülaltoodud kujul.
Seejuures
tuleb astmefunktsioonide f(A) = Ar
korral 0-maatriksist erinev vaid esimene kordseile
omaväärtustele 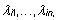 vastavaist maatrikseist Zij
ja seega
vastavaist maatrikseist Zij
ja seega
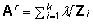 . .
Näiteks
maatriksfunktsiooni P1000 leidmiseks,
kus
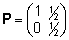 , ,
tuleb
esmalt arvutada maatriksi P omaväärtused,
lahendades järgmise võrrandi:
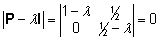 =>
=> 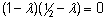 =>
=> 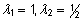 . .
Konstantsete
maatriksite Z1 ja Z2
leidmiseks tuleb konstrueerida vajalik võrrandisüsteem
ja see lahendada:
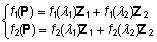 =>
=> 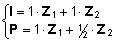 =>
=> 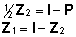
=> 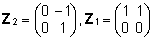 . .
Edasi
saabki arvutada P1000:
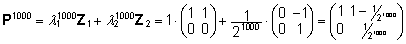 . .
Samad
konstantsed maatriksid Z1 ja Z2
on kasutatavad mistahes maatriksfunktsiooni leidmiseks,
sest algoritmi kohaselt tuleb vastavat funktsiooni
rakendada vaid omaväärtustele. Näiteks
funktsioon
P-2(P2
+ P + I) avaldub
kujul
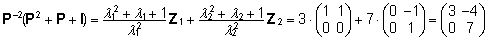 . .
|