Pöördmaatriks

Maatriksi A pöördmaatriks A^-1 on maatriks, millega esialgset maatriksit vasakult või paremalt korrutades on tulemuseks ühikmaatriks:

AA^-1 = I ja A^-1A = I.

Pöördmaatriks leidub igal mittenullilise determinandiga (mittesingulaarsel) ruutmaatriksil.

Üldine valem maatriksi A pöördmaatriksi A^-1 elementide leidmiseks on järgmine

a_ij^-1 = [(-1)^i+j | A^T_ij |] / | A |,

kus a_ij^-1 tähistab maatriksi A^-1 ij.-t elementi, A^T_ij on maatriksi A transponeeritud maatriksi A^T ij. miinor, | A^T_ij | on selle miinori determinant ja | A | on maatriksi A determinant.

Kui A on 2x2-maatriks, avaldub tema pöördmaatriks kujul

.

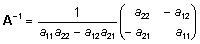Näide. .

.

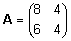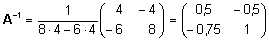Teostage ise kontroll, kas leitud pöördmaatriks rahuldab pöördmaatriksi tingimusi (AA^-1 = I ja A^-1A = I)!

Omadused

1. (A^-1)^-1 = A.
2. |A^-1| = |A|^-1, kui A on mittesingulaarne.
3. (A^T)^-1 = (A^-1)^T.
4. (ABC)^-1 = C^-1B^-1A^-1; A, B, C - mittesingulaarsed.
5. Diagonaalmaatriksi pöördmaatriks on samuti diagonaalmaatriks, kusjuures tema diagonaalielementideks on esialgse maatriksi diagonaalielementide pöördelemendid, s.t. 
   kui 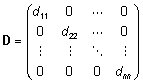 ,  siis  .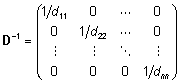

Pöördmaatriks leiab rakendust näiteks lineaarvõrrandisüsteemide lahendamisel.

Korrutades maatriksvõrduse

Ax = c

mõlemad pooled vasakult läbi kordajate maatriksi A pöördmaatriksiga, saame lahendivektori x kujul

x = A^-1c.

Näide. Olgu meil tarvis lahendada lineaarvõrranditesüsteem

.

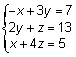Sama süsteem maatrikskujul on

,

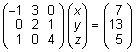millest

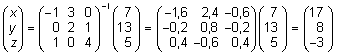
ehk x = 17, y = 8 ja z = -3.

Teostage ise kontroll. Kas leitud väärtused rahuldavad võrrandisüsteemi?