Ruutvormid, positiivne ja negatiivne määratus

Olgu a nx1-vektor ja A nxn-maatriks.

Avaldist a^Tx nimetatakse lineaarvormiks ja avaldist x^TAx ruutvormiks vektori x suhtes.

Seejuures võime alati eeldada, et maatriks A on sümmeetriline, sest kui ta seda pole, võime asendada A sümmeetrilise maatriksiga 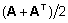ning saada esialgsega võrdse ruutvormi:

.

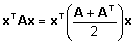Olgu nüüd maatriks A sümmeetriline.

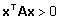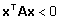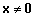• Öeldakse, et maatriks A on positiivselt määratud (negatiivselt määratud), kui   () iga korral;
   
• positiivselt poolmääratud (negatiivselt poolmääratud), kui 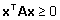  (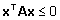) iga x korral.

Omadused

1. Kui A on positiivselt määratud, siis on seda ka A^-1.
2. Maatriks A on positiivselt määratud, kui kõik tema omaväärtused on positiivsed ().
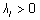3. B^TB ja BB^T on positiivselt poolmääratud, B - mxn-maatriks.