Korrutamine

Maatriksi korrutamisel skalaariga korrutatakse sellega läbi maatriksi iga element.

Näide. k = 2, .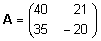

Siis .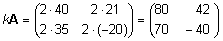

Kahte maatriksit saab omavahel korrutada, kui esimese maatriksi veergude arv on võrdne teise maatriksi ridade arvuga. 
Korrutismaatriksi ridade arv on võrdne esimese maatriksi ridade arvuga ja veergude arv teise maatriksi veergude arvuga:

C_nxm = A_nxkB_kxm.

Korrutismaatriksi element kohal ij (reas i veerus j) leitakse kui esimese maatriksi i-nda rea ja teise maatriksi j-nda veeru vastavate elementide korrutiste summa:

.

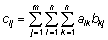Näide. , .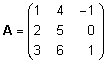

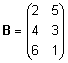Maatriksi C = AB elemendid leitakse järgmiselt:

c11 = 1x2 + 4x4 + (-1)x6 = 12	(maatriksi A 1. rida korrutatuna maatriksi B 1. veeruga),
c21 = 2x2 + 5x4 + 0x6 = 24	(maatriksi A 2. rida korrutatuna maatriksi B 1. veeruga),
c31 = 3x2 + 6x4 + 1x6 = 36	(maatriksi A 3. rida korrutatuna maatriksi B 1. veeruga),
c12 = 1x5 + 4x3 + (-1)x1 = 16	(maatriksi A 1. rida korrutatuna maatriksi B 2. veeruga),
c22 = 2x5 + 5x3 + 0x1 = 25	(maatriksi A 2. rida korrutatuna maatriksi B 2. veeruga),
c23 = 3x5 + 6x3 + 1x1 = 34	(maatriksi A 3. rida korrutatuna maatriksi B 2. veeruga).

Seega .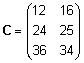

Seejuures on maatriks C 3x2-maatriks, kus 3 on maatriksi A ridade arv ja 2 on maatriksi B veergude arv.

Omadused

1. .
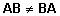2. IA = AI = A, kus I on ühikmaatriks.
3. ABC = A(BC) = (AB)C.
4. A(B + C) = AB + AC.