|
Omaväärtused
ja omavektorid
Skalaari 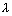 nimetatakse nxn-maatriksi A omaväärtuseks
(ladina juureks, karakteristlikuks juureks; ingl. eigenvalue),
kui leidub selline nx1 mittenulliline vektor
x, mis rahuldab võrdust
nimetatakse nxn-maatriksi A omaväärtuseks
(ladina juureks, karakteristlikuks juureks; ingl. eigenvalue),
kui leidub selline nx1 mittenulliline vektor
x, mis rahuldab võrdust
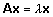 . .
Viimane võrdus
on teisiti üleskirjutatav kujul
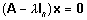 . .
Seega on 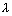 maatriksi A omaväärtus siis ja ainult siis,
kui
maatriksi A omaväärtus siis ja ainult siis,
kui 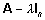 on singulaarne (st, et
on singulaarne (st, et 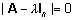 ). ).
Võrrandit 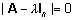 nimetatakse karakteristlikuks võrrandiks ja
selle võrrandi lahendid ongi maatriksi A
omaväärtused.
nimetatakse karakteristlikuks võrrandiks ja
selle võrrandi lahendid ongi maatriksi A
omaväärtused.
Maatriksi A kõigi
omaväärtuste hulka 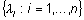 nimetatakse maatriksi A spektriks.
nimetatakse maatriksi A spektriks.
Maatriksi A omaväärtusele
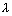 vastavat mittenullilist vektorit x nimetatakse
maatriksi A omavektoriks [ingl. eigenvector].
S.t., et mittenulliline vektor x on nxn-maatriksi
A omaväärtusele
vastavat mittenullilist vektorit x nimetatakse
maatriksi A omavektoriks [ingl. eigenvector].
S.t., et mittenulliline vektor x on nxn-maatriksi
A omaväärtusele 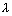 vastav omavektor siis ja ainult siis, kui ta on homogeense
lineaarvõrrandisüsteemi
vastav omavektor siis ja ainult siis, kui ta on homogeense
lineaarvõrrandisüsteemi 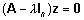 lahendiks (z suhtes).
lahendiks (z suhtes).
Omadused
- Maatriksid A
ja AT on samade omaväärtustega.
- Ruutmaatriksi A
omaväärtuste summa võrdub tema jäljega ning korrutis
determinandiga.
- Sümmeetrilise maatriksi
astak võrdub tema mittenulliliste omaväärtuste arvuga.
- Kui
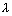 on maatriksi A omaväärtus, siis
on maatriksi A omaväärtus, siis 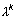 on maatriksi Ak omaväärtus.
on maatriksi Ak omaväärtus.
- Olgu B nxn-maatriks,
D diagonaalmaatriks, mille peadiagonaalil
paiknevad maatriksi B omaväärtused ning L
nxn-maatriks, mis koosneb maatriksi
B omaväärtustele vastavatest omavektoritest.
Kui L on mittesingulaarne, siis on maatriks
B avaldatav kujul
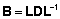 . .
Näide. 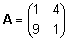 . .
Maatriksile A
vastav karakteristlik võrrand on
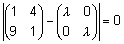 ,
s.t. ,
s.t. 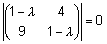 . .
Kirjutades viimase
determinandi lahti saame, et 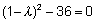 ,
millest maatriksi A omaväärtused tulevad: ,
millest maatriksi A omaväärtused tulevad:
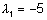 ja
ja 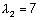 . .
Leitud omaväärtustele
vastavate omavektorite leidmine pole enam nii lihtne.
Siinkohal võiks vaid märkida, et kuna
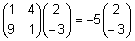 ja
ja 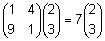 , ,
siis on vektorid 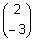 ning
ning 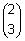 omaväärtustele -5 ning 7 vastavad omavektorid
omaväärtustele -5 ning 7 vastavad omavektorid
(rahuldavad võrdust 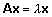 ). ).
|