Lineaarne sõltumatus ja maatriksi astak

Maatriksi astakuks [ingl. rank] nimetatakse tema maksimaalset lineaarselt sõltumatute ridade või veergude arvu. 
Maatriksi A astakut tähistatakse r(A).

Kui ruutmaatriksi astak võrdub tema ridade või veergude arvuga, siis öeldakse, et maatriks on täisastakuga.

Kui ruutmaatriks ei ole täisastakuga, siis tema determinant võrdub nulliga ja pöördmaatriksit ei eksisteeri (maatriks on singulaarne).

Omadused

1. r(A) = r(A^T) = r(A^TA) = r(AA^T).
2. Kui A on pxq-maatriks, siis .
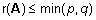3. Kui A ja B on pxq-maatriksid, siis .
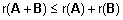4. Kui A on pxq-maatriks ja B qxr-maatriks, siis .

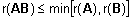Näide. .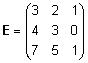

Maatriksi E astak r(E) = 2, sest kolmas rida avaldub kahe esimese rea summana ja seega ei saa lineaarselt sõltumatuid ridu olla rohkem kui kaks. Seega ka |E| = 0 ja pöördmaatriksit E^-1 ei leidu.