Ülesanded

1. Teil on vaja hinnata aretusväärtused kümnele omavahel suguluses mitteolevale loomale. Vahendeid (rahalisi, ajalisi jne) on määramaks 20 fenotüübiväärtust.
   Oletame, et kõigil loomadel on fenotüübiväärtused soovi korral määratavad korduvalt, samuti on fenotüübiväärtusi võimalik määrata nii looma emal, järglastel kui ka poolõdedel.

   Milline fenotüübiväärtuste määramise strateegia annab täpseimad aretusväärtuste hinnangud, kui

   a) h² = 0,25, R = 0,5 ja c² = 0;

   b) h² = 0,25, R = 1 ja c² = 0;

   c) h² = 0,25, R = 0,5, c² = 0 ja loomal enesel pole fenotüübiväärtuste määramine võimalik.

   Lahendamiseks kasutage programmi stselind_est.xls.
   NB! Juhul, kui teil tekib probleeme antud faili avamisega või rakendamisega, on probleem ilmselt teie arvuti MS Office turvaseadetes (makrod pole lubatud). Lahendusena tuleks Excelil lubada antud faili sisu (makrode) kasutamist.
   Makrode lubamisest ja keelamisest MS Excelis vt näiteks
   http://office.microsoft.com/et-ee/excel-help/HA010354316.aspx
    

2. Uurige, kuidas sõltub isa aretusväärtuse hinnangu täpsus tema järglaste arvust ja päritavuskoefitsiendi
   väärtusest.

   a) Konstrueerige Excelis tabel, kuhu pange kirja potentsiaalsed järglaste arvud n, huvi pakkuvad
   päritavuskoefitsiendi h² väärtused ja arvutage valemist

   

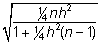
   isa aretusväärtuse hinnangu täpsus.

   Potentsiaalne järglaste arv võiks varieeruda 1-st 100-ni ja aretusväärtuse hinnangute täpsused
   arvutage h² = 0,2, h² = 0,5 ja h² = 0,8 korral.
   Illustreerige modelleerimise tulemusi joonisega.

   b) Millal on aretusväärtuse hindamiseks (täpsuse seisukohast) vaja rohkem järglasi, h² = 0,2,
   h² = 0,5 või h² = 0,8 korral?

   c) Vähemalt kui mitut järglast on vaja, et isa aretusväärtuse hinnangu täpsus oleks vähemalt 0,8
   (eraldi h² = 0,2, h² = 0,5 ja h² = 0,8 korral)?
    

3. Kolmest huvi pakkuvast eesti tumedapealisest jäärast ühel on kolm, teisel kaks ja kolmandal üks poolõde (jäär ja tema poolõed on ühise isa järglased), kellel kõigil on registreeritud 100 päeva mass ja tallede arv esimesel poegimisel.

Andmed on esitatud järgmises tabelis.

Jäär	Utt	100 päeva mass	Tallede arv
I	1	22,8	1
I	2	26,2	2
I	3	24,7	1
II	4	26,1	2
II	5	22,5	2
III	6	27,9	1

a) Hinnake jäärade aretusväärtused mõlema tunnuse osas ja arvutage kõigile jääradele nende aretusväärtuste hinnangute täpsus (accuracy). Poolõdedele ühine keskkonnaefekt lugege võrdseks nulliga, c²_HS = 0 (eeldatavalt on vaatlusalused poolõed pärit eri lautadest jmt).

Arvutused võite näiteks koondada järgnevat tüüpi tabelitesse (siin näide 100 päeva massi tarvis).

Jäär	Poolõdede arv (n)	100 päeva mass
		Kordaja selektsiooni-indeksis (b)	Poolõdede keskmine	Poolõdede keskmise erinevus pop. keskmisest	Aretusväärtus (AV)	Aretusväärtuse hinnangu täpsus (r)
I
II
III

Arvutusteks vajalikud populatsiooni keskmised väärtused ja päritavuskoefitsiendid on kirjas järgnevas tabelis.

Tunnus	Baaspopulatsiooni		Päritavus (h2)
	keskmine	standardhälve
100 päeva mass	25,3	2,76	0,5
Sündinud tallede arv	1,51	0,32	0,1

b) Hinnake kõigile jääradele suhteline aretusväärtus (kasumiindeksi väärtus) juhul, kui majanduslikud kaalud 100 päeva massile ja sündinud tallede arvule on vastavalt 0,25 ja 0,75.

c) Teisendage suhtelisi aretusväärtuseid nii, et nende keskmine oleks 100 ja standardhälve 10 punkti. Teisendamisel lähtuge sellest, et baaspopulatsioonis (mille suhtes on vaja populatsiooni geneetiliselt hinnata) on keskmine suhteline aretusväärtus 0 standardhälbega 1,5.
Järjestage jäärad suhteliste aretusväärtuste alusel. Arvutused võite näiteks koondada järgnevat tüüpi tabelisse.

Jäär	100 päeva massi aretusväärtus (AV100)	Viljakuse aretusväärtus (AVv)	Suhteline aretusväärtus (SAV = 0,25AV100 + 0,75AVv)	Teisendatud suhteline aretusväärtus	Jäära järjekorranumber
I
II
III