Mitmene selektsiooniindeks korrelleeruvate tunnuste korral

Mitmele informatsiooniallikale tuginevate aretusväärtuse hinnangute puhul leitakse selektsiooniindeksi parameetrid maatriksvõrdusest (3).

Juhul, kui selektsioon baseerub ühel tunnusel, mõõdetud on aga mitut tunnust, mis selektsiooni aluseks olevaga tugevalt korreleeruvad ja võimaldavad seeläbi täpsustada aretusväärtuse hinnangut, on mõttekas kaasata selektsiooniindeksisse kõik tunnused, mille kohta infot omatakse.

Olgu meil mõõdetud fenotüüp kahe tunnuse osas, P₁ ja P₂, ning baseerugu selektsioon teisel tunnusel. Eesmärk on konstrueerida selektsiooniindeks prognoosimaks aretusväärtusi tunnusele P₂ arvestades mõlema tunnuse mõõtmisi:

.

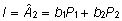Kaaluparameetrite b₁ ja b₂ arvutamiseks peame välja kirjutama maatriksvõrduse (2):

.

Võrduse paremal poolel asuva vektori elemendid avalduvad lineaarse geneetilise mudeli, päritavuskoefitsiendi ja geneetilise korrelatsioonikordaja definitsioonidest lähtuvalt kujul

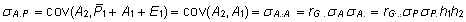
ja

.

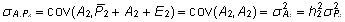Võrduse vasakpoolses maatriksis paiknevad fenotüübilised kovariatsioonid saab avaldada fenotüübiliste korrelatsioonide kaudu: 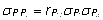. Kokkuvõttes saame indeksi kaaluparameetrid leida maatriksvõrdusest :

.

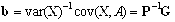(14)

Näide. Jätkame peatüki 3 näidet veiste ööpäevasest juurdekasvust (P₁) ja söödakasutuse efektiivsusest (P₂).

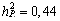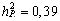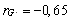Oletame nüüd, et mõlema tunnuse väärtused on mõõdetud ning selektsiooni aluseks olevaks tunnuseks, millele tahame hinnata aretusväärtusi, on endiselt söödakasutusvõime. Olgu lisaks juba toodud parameetritele (, , , ja ) teada ka fenotüübiline korrelatsioon tunnuste vahel: .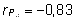

Asendades dispersioonid ja kovariatsioonid valemis (14) nende arvväärtustega, saame indeksi kaaluparameetriteks

,

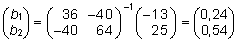mille alusel selektsiooniindeks on

.

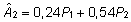Sellisel kujul leitud indeksis vastab nii suuremale juurdekasvule kui ka suuremale söödakulule suurem indeksi väärtus (vaikimisi konstrueeritakse selektsiooniindeksid alati nn positiivses suunas -- mida suurem on indiviidil mõõdetud tunnuse väärtus võrreldes populatsiooni keskmisega, seda parem). Et parimateks loetakse ikkagi vähima söödakuluga loomi, tuleks antud juhul selekteerida välja väiksema indeksi väärtusega (söödakulu aretusväärtusega) loomad.

Hinnatud aretusväärtuse täpsus avaldub kujul

.