|
Aretusväärtuse
prognoosimine looma korduvalt mõõdetud fenotüübiväärtuste
alusel
Eeldame,
et indiviidil on selektsiooni aluseks oleval tunnusel
sooritatud n mõõtmist ning kõigi
mõõtmiste dispersioon on sama nagu ka
kõigi mõõtmiste vahelised keskkonnamõjudest
tingitud korrelatsioonid (kõik sama looma mõõtmiste
vahelised geneetilised korrelatsioonid võrduvad
ühega, sest tegu on ju ühe ja sama tunnusega,
mis on mõjutatud samade geenide poolt).
Tähistame
indiviidi i mõõtmiste keskmise
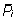 .
Vaatlusaluse looma i aretusväärtus
on siis avaldatav seosena .
Vaatlusaluse looma i aretusväärtus
on siis avaldatav seosena
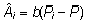 . . |
(12)
|
kus
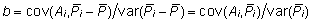 . .
Et
indiviidil i sooritatud j. mõõtmise
tulemus Pij avaldub kujul 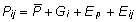 (genotüübiefekt Gi ja
püsiv keskkonnaefekt
(genotüübiefekt Gi ja
püsiv keskkonnaefekt 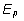 on kõigil mõõtmistel samad ega
sõltu seega konkreetse mõõtmise
järjekorranumbrist j), siis avaldub n
mõõtmise keskmine seosena
on kõigil mõõtmistel samad ega
sõltu seega konkreetse mõõtmise
järjekorranumbrist j), siis avaldub n
mõõtmise keskmine seosena 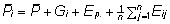 ,
kus Eij on mõõtmisele
j vastav juhuslik keskkonnamõju. Seega ,
kus Eij on mõõtmisele
j vastav juhuslik keskkonnamõju. Seega

ja,
eeldades genotüübi ning püsiva ja juhuslikku
keskkonnamõju sõltumatust,
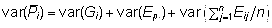 . .
Arvestades,
et kõik juhuslikud vead Eij
on eeldatavalt sama dispersiooniga, avaldub viimane
liidetav vastavalt dispersiooni omadustele kujul
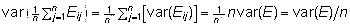 . .
Et
vastavalt korduvuse definitsioonile 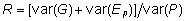 ja sellest järelduvalt
ja sellest järelduvalt
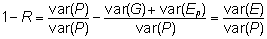 , ,
siis
 . .
Seega
avaldub selektsiooniindeksi (12) kordaja b
kokkuvõtteks seosest
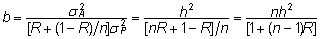 . .
Indeksi
täpsus on tänu seosele (5.7) leitav valemist
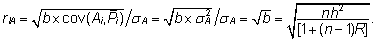
Joonisel
1 on kujutatud indiviidi aretusväärtuse
hinnangu täpsust sõltuvalt mõõtmiste
arvust ning päritavuskoefitsiendi ja korduvuse
väärtustest. Mida suurem on päritavuskoefitsiendi
väärtus ja mida rohkem on sooritatud mõõtmisi,
seda täpsem on aretusväärtuse hinnang.
Korduvuse kõrge väärtus pärsib
lisamõõtmiste positiivset mõju
aretusväärtuse hinnangu täpsusele --
see on ka loomulik, sest kõrge korduvuse korral
on kõigi samal indiviidil sooritatud mõõtmiste
tulemused üsna sarnased ega sisalda märkimisväärselt
lisainformatsiooni, mida saaks ära kasutada aretusväärtuse
hindamiseks. Lisamõõtmiste positiivne
efekt aretusväärtuse hinnangu täpsusele
ilmneb eelkõige madala päritavuse ja korduvuse
korral, kõrge päritavuse ja eelkõige
kõrge korduvuse korral ei ole lisamõõtmistel
erilist mõtet.
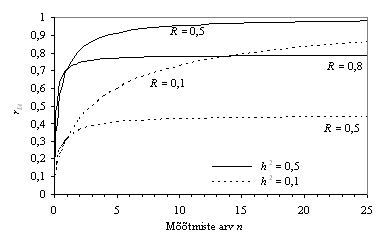
Joonis
1. Indiviidi aretusväärtuse hinnangu täpsus
sõltuvalt mõõtmiste arvust
ning päritavuskoefitsiendi ja korduvuse väärtustest.
Näide.
Eeldame, et lehm Roosi kolme esimese laktatsioonikuu
keskmine piimatoodang oli 7000 kg. Leiame Roosi
piimatoodangu aretusväärtuse eeldusel,
et karja keskmine sama perioodi piimatoodang oli
6000 kg, esimese 3 kuu piima-toodangu päritavus
on 0,3 ja korrelatsioon 3 kuu toodangute vahel (korduvus)
on 0,5.
Vastavalt valemile (12) saame:
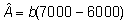 , ,
kus
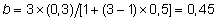 , ,
millest
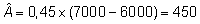 kg.
kg.
Aretusväärtuse
hinnangu täpsuseks saame 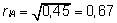 . .
|