Vastused ja lahendused

1. 16-l mullikal on fikseeritud nende tiinestuvus esimesest seemendusest ning lisaks on nad genotüpiseeritud teatud lookuste osas. Uurimaks seost mullikate tiinestumise ja ühe konkreetse genotüübi vahel, konstrueeriti järgmine sagedustabel.

Genotüüp	Ei tiinestunud	Tiinestus	Kokku
AA	2	5	7
AG	8	1	9
Kokku	10	6	16

a) Arvutage toodud tabeli alusel tiinestuvuskordajad ("risk tiinestuda"), riskisuhted ja šansside suhted ning sõnastage nende alusel mõned laused.

Vastus: genotüübiga AA lehmade tiinestuvuskordaja on 0,714 ja genotüübiga AG lehmade tiinestuvuskordaja on 0,111, st et genotüübiga AA lehmadest tiinestus 71,4% ja genotüübiga AG lehmadest 11,1%.
Riskisuhe RR = 6,43 tähendab, et genotüübiga AA lehmadel on "risk" tiinestuda 4,43 korda suurem, võrreldes genotüübiga AG lehmadega.
Šansside suhte OR = 20,0 alusel võib väita, et genotüübiga AA lehmadel on šanss tiinestuda 20 korda suurem, võrreldes genotüübiga AG lehmadega.

b) Arvutage šansside suhte 95%-usaldusintervall ja sõnastage järeldus seose statistilise olulisuse kohta.

Vastus: Šansside suhte 95%-usaldusintervall 95%CI_OR = (1,42; 282,46) näitab, et genotüübiga AA lehmade tiinestumine erineb statistiliselt oluliselt genotüübiga AG lehmade tiinestumisest (sest 95%-usaldusintervall ei sisalda arvu 1).

c) Teostage χ²-test ja sõnastage järeldus seose statistilise olulisuse kohta.

Vastus: p = 0,0134 < 0,05, seega on seos uuritava genotüübi ja lehmade tiinestumise vahel statistiliselt oluline.

d) Teostage Fisheri täpne test (näiteks mõne online-kalkulaatori abil) ja sõnastage järeldus seose statistilise olulisuse kohta.

Vastus: ühepoolsele testile vastav olulisuse tõenäosus p = 0,024, kahepoolsele testile vastav olulisuse tõenäosus sõltuvalt arvtamise metoodikast p = 0,035 või p = 0,049. Seega on seos uuritava genotüübi ja lehmade tiinestumise vahel statistiliselt oluline.

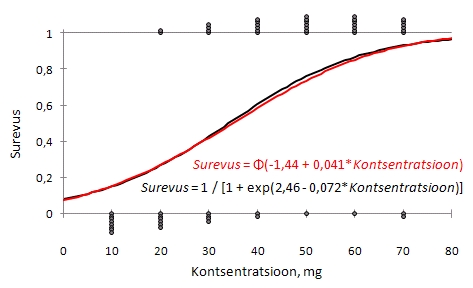
2. Uuriti kahjurite surevust sõltuvalt kahjuritõrjevahendi kontsentratsioonist. Uuringu andmed ning logistilise ja probit-regressiooni tulemused on esitatud järgmisel joonisel.

a) Leidke 90%-lise tõenäosusega surmav kontsentratsioon (LC90, 90% lethal concentration) nii logistilise kui ka probit-regressiooni alusel.

Vastus:

logistilise mudeli kohaselt Surevus = 1 / [1 + exp(2,46 - 0,072*Kontsentratsioon)], mistap 90%-liselt surmav kontsentratsioon

LC90 = {LN[0,9/(1-0,9)] + 2,46}/0,072 = 64,68 mg;

probit-mudeli kohaselt Surevus = Φ(-1,44 + 0,041*Kontsentratsioon), mistap 90%-liselt surmav kontsentratsioon

LC90 = [Φ^-1(0,9) + 1,44]/0,041 = (1,28+1,44)/0,041 = 66,38 mg.

b) Kui suur on šansside suhe ja mida see näitab?

Vastus: OR = e^0,072 = 1,075, seega suureneb kahjuritõrjevahendi kontsentratsiooni suurenemisel 1 mg võrra šanss, et kahjur sureb, 1,075 korda.

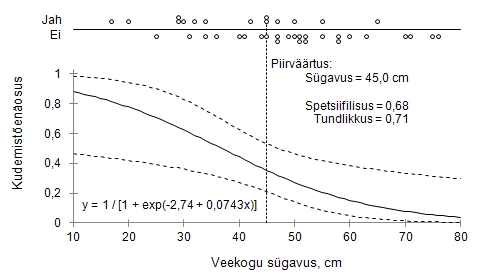
3. Uuriti, kui sügavates veekogudes armastab kudeda mudakonn. Uuringu andmed ning logistilise regressioonanalüüsi tulemused on esitatud järgmisel joonisel.

a) Millisele hinnangulisele kudemistõenäosusele vastab kudemiseks sobivaid ja mittesobivaid veekogusid optimaalseimalt eristav sügavuse piirväärtus 45 cm?

Vastus: kudemiseks sobivaks võib veekogu lugeda juba siis, kui logistilisest mudelist hinnatud kudemiseks sobivuse tõenäosus on üle 0,35.

b) Mitu korda väheneb kudemise šanss veekogu sügavuse suurenemisel 1 cm võrra?

Vastus: OR = e^-0,0743 = 0,928, seega väheneb veekogu sügavuse suurenemisega 1 cm võrra šanss sobida mudakonnale kudemiseks 0,928 korda.

c) Mida tähendab, et antud mudeli tundlikkus on 0,71 ja spetsiifilisus 0,68?

Vastus: 45 cm-st madalamad on 71% kudeveekogusid ja 45 cm-st sügavamad on 68% kudemiseks mittevalitud veekogusid.

d) Kui teada on, et ROC-kõvera alune pindala on AUC = 0,74 ja 95%CI_AUC = (0,58;0,91), siis kui hästi võimaldab veekogu sügavus prognoosida selle sobivust mudakonnale kudemiseks ja kas vastav seos on statistiliselt oluline?

Vastus: otsustades veekogu sobivuse üle mudakonnale kudemiseks üksnes veekogu sügavuse järgi, on prognoosi täpsus rahuldav (AUC = 0,74), samas on seos veekogu sügavuse ja kudemistõenäosuse vahel on statistiliselt oluline (p<0,05, usaldusintervall ei sisalda arvu 0,5).