Peatükkides
2.1-2.7
näitena vaadatud koerte andmestiku puhul on
mudel, hindamaks soo mõju ravi tulemusele,
logistilise mudelina esitatav kujul
logit(pij)
= μ + Si + eij,
kus
pij on i. sugu j. koera terveks
mittesaamise tõenäosus (i=1,2;
j=1,..., 25), μ on mudeli vabaliige,
Si on i. soo mõju
ja eij on mudeli viga.
Kui
mudeli vabaliige ja soo mõjud on andmeist
hinnatud, avaldub terveks mittesaamise tõenäosus
kujul
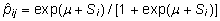 .
.
Võttes
isaseks olemise efekti parameetrite ühese hindamise
tarvis võrdseks nulliga (isane olemine on
sellisel juhul nö baastase ja mudeliga hinnatakse
emaseks olemise efekti selle suhtes), tuleb mudeli
vabaliikme hinnanguks -1,61 ja emaseks olemise mõju
hinnanguks 2,42.
Terveks
mittesaamise tõenäosused sõltuvalt
koera soost avalduvad kujul
P(haige|sugu=E)
= exp(-1,61 + 2,42)/[1 + exp(-1,61 + 2,42)] = 0,69
ja
P(haige|sugu=I)
= exp(-1,61 + 0)/[1 + exp(-1,61 + 0)] = 0,17
ning
võrduvad arvuliselt terveks mittesaanud koerte
suhteliste sagedustega eraldi emaste ja isaste koerte
hulgas (vt peatüki
2.2 näite esimene tabel).
Šansside
suhe, mis avaldub sarnaselt logistilisele regressioonile
mudeli parameetri eksponentfunktsioonina:
OR
= exp(2,42) = 11,25,
näitab,
et šanss mitte terveks saada on emastel koertel
11,25 korda kõrgem, kui isastel koertel.
Ka selle, antud juhul logistilisest mudelist leitud
parameetri väärtus, on identne peatükis
2.5 kahemõõtmelisest sagedustabelist
leitud šansside suhte väärtusega.