Hii-ruut test

Klassikaliseim kahemõõtmelise sagedustabeli alusel teostav test, otsustamaks tabelis esitatud tunnuste seotuse statistilise olulisuse üle, on χ²-test (hii-ruut test; ingl. chi-square test või Pearson's goodness-of-fit test).

χ²-test võrdleb andmete alusel konstrueeritud sagedustabelit nö ideaalse, sõltumatuse juhule vastava, sagedustabeliga. Viimases avalduvad sagedused kujul n_i.n_.j/n (vt punkt 2.3).

Testitav hüpoteeside paar on kujul:

H₀: tunnused on sõltumatud ehk potentsiaalne riskifaktor ei mõjuta uuritava sündmuse toimumist,
H₁: tunnused on sõltuvad ehk potentsiaalne riskifaktor mõjutab uuritava sündmuse toimumist;

ehk matemaatilisel kujul:

H₀: n_ij = n_i.n_.j/n,
H₁: n_ij ≠ n_i.n_.j/n.

Teststatistikut, mis mõõdab erinevust nullhüpoteesile vastava ja tegeliku sagedustabeli vahel ning mis nullhüpoteesi kehtides on ligikaudu χ²-jaotusega vabadusastmete arvuga (m-1)(k-1), nimetatakse χ²-statistikuks ja see avaldub kujul

,

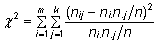kus m ja k on uuritavate tunnuste erinevate väärtuste arvud. Binaarse uuritava tunnuse ja kaheväärtuselise faktortunnuse tarvis konstrueeritava 2x2-sagedustabeli puhul on teststatistik χ²-jaotusega vabadusastmete arvuga üks.

Seega summeeritakse χ²-statistiku väärtuse leidmiseks kõigi tegelike ja sõltumatuse juhule vastavate sageduste ruuterinevus, mis on täiendavalt läbi jagatud sõltumatuse juhule vastavate sagedustega.

Otsuse vastu võtmine, kumb hüpoteesidest kehtib, käib tänapäeval enamasti olulisuse tõenäoses p alusel, mis leitakse kui tõenäosus, et vastava χ²-jaotusega suurus võib omandada teststatistiku väärtusega võrdse või suurema väärtuse. Kui p≤0,05, loetakse traditsiooniliselt tõestatuks alternatiivne hüpotees H₁, kui aga p>0,05, jäädakse nullhüpoteesi H₀ juurde.

Kuna χ²-testil leitav teststatistik on nullhüpoteesi kehtides χ²-jaotusega vaid ligikaudu, ei sobi χ²-test väga väikeste valimite analüüsimiseks. Enamasti pannakse χ²-testi eeldusena kirja, et kõik oodatavad sagedused n_i.n_.j/n peaksid olema suuremad-võrdsed viiest.

Koerte näite puhul võib testitava hüpoteeside paari sõnastada kujul:

H₀: ravi tulemus ei sõltu koera soost,
H₁: ravi tulemus on soospetsiifiline.

χ²-statistiku väärtuse arvutamiseks vajalikud sagedustabelid tegelike ja nullhüpoteesile vastavate sagedustega on kujul (vt punkt 2.3)

	Ei saanud terveks	Sai terveks
Emane	9	4
Isane	2	10

ja

	Ei saanud terveks	Sai terveks
Emane	5,72	7,28
Isane	5,28	6,72

Suurused (n_ij - n_i.n_.j/n)² / (n_i.n_.j/n) iga sagedustabeli lahtri tarvis on kirjas järgmises tabelis

	Ei saanud terveks	Sai terveks
Emane	1,60	2,04
Isane	1,48	1,8

millest χ² = 1,60+1,48+2,04+1,88 = 6,997.

Ühe vabadusastmega χ²-jaotuse puhul on sellele teststatistiku väärtusele vastav olulisuse tõenäosus p = 0,008, mistap võib lugeda tõestatuks alternatiivse hüpoteesi: ravi tulemus on soospetsiifiline (ehk seos ravi tulemuse ja koera soo vahel on statistiliselt oluline).

Valik online-kalkulaatoreid, mis pakuvad χ²-testi teostamise võimalust:

• http://vassarstats.net/ -> Frequency data
• http://www.quantitativeskills.com/sisa/statistics/two2hlp.htm
• http://www.physics.csbsju.edu/stats/contingency.html
• http://home.ubalt.edu/ntsbarsh/Business-stat/otherapplets/Catego.htm
• http://www.healthstrategy.com/epiperl/epiperl.htm (lisaks palju erinevaid karakteristikuid)
• http://statpages.org/ctab2x2.html (lisaks väga palju erinevaid karakteristikuid)