Probit-regressioon

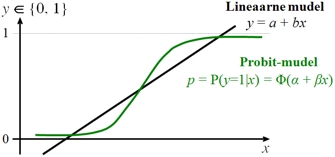
Analoogselt logistilisele regressioonile prognoosib ka probit-regressioon (ingl. probit-regression) uuritava sündmuse toimumise tõenäosust ja selle muutumist sõltuvalt pideva argumenttunnuse väärtuse muutumisest ning saadavad prognoosid jäävad alati 0 ja 1 vahele (vt järgmine joonis).
 

Funktsioonina, mis projitseerib mistahes reaalarvulise väärtuse vahemikku (0,1), kasutab probit-regressioon standardse normaaljaotuse jaotusfunktsiooni, mida traditsiooniliselt tähistatakse tähega Φ.

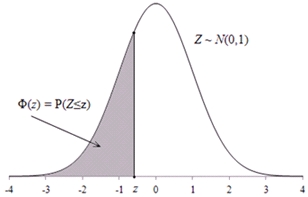
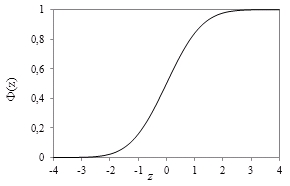
Jaotusfunktsiooni Φ väärtus kohal z kujutab enesest tõenäosust, et standardse normaaljaotusega juhuslik suurus Z omandab väärtuse, mis on väiksem või võrdne z-st (vt alljärgnev vasakpoolne joonis): Φ(z) = P(Z≤z), Z ~ N(0,1). Alljärgneval parempoolsel joonisel on aga esitatud standardse normaaljaotuse jaotusfunktsiooni graafik.
 

Probit-regressiooni mudel (probit-mudel) kirja panduna sündmuse toimumise tõenäosuse p = P(y=1) tarvis on järgmine:

p = P(y=1|x) = Φ(α + βx).

Alternatiivne esitus on lineaarse võrrandina standardse normaaljaotuse jaotusfunktsioon pöördfunktsiooni ehk probit-funktsiooni suhtes (siit ka probit-regressiooni nimetus):

probit(p) = Φ^-1(p) = α + βx.
 

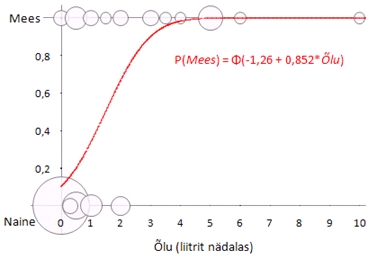
Püüdes prognoosida tudengi meheksolemise tõenäosust nädalas keskmiselt tarbitava õllekoguse alusel probit-regressiooniga, on tulemuseks regressioonivõrrand

P(Mees) = Φ(-1,26 + 0,854*Õlu).

See, et tarbitava õllekoguse kordaja mudelis, 0,854, on positiivne arv, näitab, et mida enam tudeng õlut joob, seda suurema tõenäosusega ta mees on. Hinnatud probit-regressiooni võrrand koos algandmetega on esitatud järgneval joonisel: