|
Juhtude
esinemissagedus ja riskisuhe
Juhtude
esinemissagedus ehk risk (epidemioloogias haigestumuskordaja;
ingl. incidence rate, rate)
leitakse iga riskifaktori taseme tarvis kui juhtude
esinemise arv jagatuna kõigi antud tasemele
vastavate vaatluste arvuga.
Kui
tegu on 2x2-tabeliga kujul
| |
Juht
|
Kontroll
|
Kokku
|
| Eksponeeritud |
a
|
b
|
a+b
|
| Mitteeksponeeritud |
c
|
d
|
c+d
|
| Kokku |
a+c
|
b+d
|
n
= a+b+c+d
|
avalduvad
juhtude esinemissagedused ehk riskid suhetena a/(a+b)
ja c/(c+d).
Riskisuhe
(ingl. risk ratio, relative risk;
RR) avaldub suhtena
RR
= (juhu risk eksponeeritutel)/(juhu risk mitteeksponeeritutel),
ehk,
kasutades tabelis toodud tähistusi,
RR
= [a/(a+b)] / [c/(c+d)].
Et
mitteeksponeerituid käsitletakse nö baasgrupina
(vt punkt 1.1),
on nende puhul riskisuhte väärtuseks üks.
Juhul, kui võrreldavaid gruppe on enam kui
kaks, leitakse riskisuhe tavaliselt kas vähima
juhtude esinemissagedusega rea (faktori taseme) või
siis sisulistel kaalutlustel nö baasina ehk referentsgrupina
käsitletava faktori taseme suhtes.
Riskisuhte
alusel järelduste sõnastamine lähtub
sellest, et
- kui
sündmuse toimumise esinemissagedus võrreldavais
gruppides on ühesugune, on riskisuhte väärtuseks
üks (RR = 1),
- kui
riskisuhte väärtus on ühest suurem
(RR > 1), on uuritava sündmuse toimumise
sagedus eksponeerituil (katsegrupis) suurem, kui
mitteeksponeerituil (kontrollgrupis),
- kui
riskisuhte väärtus on aga ühest väiksem
(RR < 1), on uuritava sündmuse toimumise
sagedus eksponeerituil (katsegrupis) väiksem,
kui mitteeksponeerituil (kontrollgrupis).
Otsustamaks
võrreldavate gruppide vahelise erinevuse statistilise
olulisuse üle, võib kasutada riskisuhte
95%-list usaldusintervalli (ingl. confidence
interval; CI):
- kui
erinevuse puudumisele (nullhüpoteesile) vastav
arv 1 jääb usaldusintervalli sisse, ei
ole katse- ja kontrollgrupi vaheline erinevus statistiliselt
oluline (1Î95%CIRR
-> p>0,05),
- kui
aga usaldusintervall arvu 1 ei sisalda, on katse-
ja kontrollgrupi vaheline erinevus statistiliselt
oluline (1Ï95%CIRR
-> p<0,05).
95%-line
usaldusintervall riskisuhtele on ligikaudu
hinnatav valemist
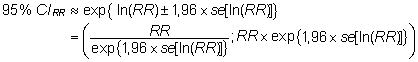 , ,
kus
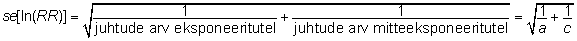 . .
Koerte
näites
| |
Ei
saanud terveks
|
Sai
terveks
|
Kokku
|
| Emane |
9
|
4
|
13
|
| Isane |
2
|
10
|
12
|
| Kokku |
11
|
14
|
25
|
on terveks mittesaamise risk emastel koertel 9/(9+4)
= 0,69 ja isastel koertel 2/(2+10) = 0,17.
Riskisuhe
avaldub aga kujul
RR
= [9/(9+4)] / [2/(2+10)] = 4,15.
Seega
on emastel koertel 4,15 korda suurem risk terveks
mitte saada.
95%-lised
usalduspiirid riskisuhtele tulevad (0,90; 19,23).
Et arv üks sisaldub leitud 95%-lises usaldusintervallis,
ei ole olulisuse nivool 0,05 alust väita, nagu
erineks terveks mittesaamise risk emastel ja isastel
statistiliselt oluliselt.
Valides
faktori sugu baastasemeks hoopis isased, tuleb riskisuhteks
RR
= [2/(2+10)] / [9/(9+4)] = 0,24.
See
tähendab, et isastel koertel on risk terveks
mitte saada 0,24 korda väiksem, kui emastel
koertel. 95%-line usaldusintrevall tuleb sellisel
juhul (0,05; 1,11), mis ei anna samuti alust lugeda
soo ja ravi tulemuse seotust tõestatuks.
|