|
Logit-
vs probit-regressioon ning tulemuste
illustreerimine
Kas
kasutada binaarse tunnuse väärtuste prognoosimiseks
logistilist või probit-regressiooni sõltub
suuresti uurimisvaldkonnast ja seal valitsevaist traditsioonidest,
vahest ka kasutatavast tarkvarast. Tõenäosuste
hinnangutel vahe peaaegu puudub (vrdl. ka tudengi
meheksolemise tõenäosuse hinnanguid järgmistel
joonistel).
Logistilise
regressiooni täiendav tulemus on šansside
suhe.
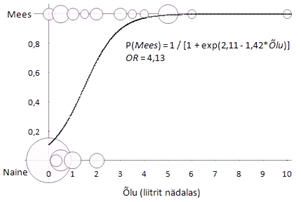 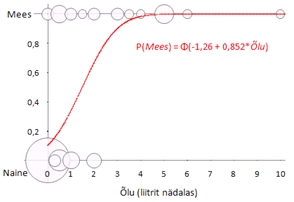
Nii
logistilise kui ka probitregressiooni tulemuste illustreerimiseks
sobib sarnaselt lineaarsele regressioonanalüüsile
kasutada jooniseid, kus on näidatud nii algandmed
kui prognoosivõrrandi graafik. Ainult erinevalt
lineaarsest regressioonanalüüsist, kus uuritaval
tunnusel on enamasti palju erinevaid väärtusi,
mis joonisel ei kattu, tuleb binaarse uuritava tunnuse
puhul näha pisut lisavaeva esitamaks algandmeid
eristatavalt. Lahenduseks on kas kasutada tavalise
punktdiagrammi asemel mulldiagrammi, kus mulli suurus
näitab mingite ühesuguste väärtuste
hulka, või esitada paralleelselt prognoosivõrrandi
graafikuga teine mittekattuvate algandmete graafik.
Kuidas seda Excelis teha, on õpetatud järgmistel
internetilehtedel:
|