Logistiline regressioon

Logistiline regressioon (ingl. logistic regression) või üldisemalt logistiline mudel ehk logit-mudel prognoosib uuritava sündmuse toimumise tõenäosust ja selle muutumist sõltuvalt pideva argumenttunnuse väärtuse muutumisest.

Kuigi binaarse, väärtustega 0 ja 1, tunnuse modelleerimiseks võib kasutada ka lineaarset regressioonivõrrandit kujul

y = a + bx

(regressioonikordajatele vähimruutude printsiipi rahuldavate hinnangute saamiseks ei ole muid piiranguid, kui et nii uuritav ehk sõltuv tunnus y kui ka argument- ehk sõltumatu tunnus x peavad olema arvulised), ei garanteeri lineaarne regressioonanalüüs saadavate prognooside jäämist mõistlikku vahemikku 0-st 1-ni. Seevastu logistilise regressiooni abil leitud tõenäosuste hinnangud jäävad alati 0 ja 1 vahele (vt järgmine joonis).
 

Logistilise regressiooni mudeli (logit-mudeli), mis binaarse tunnuse y suhtes on tegelikult mittelineaarne mudel (nagu näha ka eelnevalt jooniselt), võib esitada mitmel erineval viisil.

Üks variant on panna mudel kirja uuritava sündmuse toimumise tõenäosuse p = P(y=1) tarvis kujul

p = P(y=1|x) = exp(α + βx)/[1 + exp(α + βx)] = 1 / [1 + exp(–α – βx).

Alternatiivne esitus on logit-funktsioonina kujul

ln[p/(1-p)] = logit(p) = α + βx.

• Logistilise regressiooni võrrandi parameetrite tõlgendamine lähtub tõsiasjast, et suhe p/(1-p) kujutab enesest huvipakkuva sündmuse toimumise šanssi -- näitab, kui mitu korda tõenäolisem on uuritava sündmuse toimumine võrreldes sündmuse mittetoimumisega.
   
• Suurus ln[p/(1-p)] on siis logaritmiline šanss (ingl. log odds).
   
• Juhul, kui uuritava sündmuse toimumine on samaväärne sündmuse mittetoimumisega, st et p = 1 - p = 0,5, siis võrdub šanss ühega: p/(1-p) = 1, ja logaritmiline šanss nulliga: ln[p/(1-p)] = 0 (sest ln(1) = 0). Logistilise regressiooni kontekstis vastab šansi ühega võrdumine olukorrale, kus α + βx = 0.
   
• Logistilise regressioonivõrrandi kordaja β eksponent e^β näitab, kui mitu korda muutub sündmuse toimumise šanss argumendi muutumisel ühe ühiku võrra. Tuleneb see logistilise regressiooni võrrandist, mille kohaselt p/(1-p) = e^{α + βx} ja millest omakorda järeldub, et

e^{α + β(x+1)} = e^αe^βxe^β = e^{α + βx}e^β = e^β[p/(1-p)]

(x-i suurenemine ühe võrra muudab šanssi e^β korda).

• Seega kujutab kordaja β eksponent e^β enesest šansside suhet: e^β = OR.

  Näiteks kui e^β = OR = 2, siis kaasneb argumenttunnuse väärtuse suurenemisega ühe võrra sündmuse toimumise šansi kahekordne suurenemine (sündmuse toimumine muutub sündmuse mittetoimumisega võrreldes kaks korda tõenäolisemaks).
  Negatiivse regressioonikordaja β korral šansside suhe väheneb, sest e^β = OR < 1. St, et mida suurem on argumenttunnuse x väärtus, seda ebatõenäolisem on huvipakkuva sündmuse toimumine võrreldes sündmuse mittetoimumisega.

• Eelnevast tulenevalt on ka loomulik, et kui kordaja β on positiivne, siis argumentunnuse x väärtuse suurenedes suureneb ka uuritava sündmuse tõenäosus (tegu on positiivse seosega), kui aga kordaja β on negatiivne, siis argumentunnuse x väärtuse suurenedes uuritava sündmuse tõenäosus väheneb (tegu on negatiivse seosega).
   

Vaatame näitena andmestikku 66 tudengi vastustest nende soo ja nädalas keskmiselt joodava õllekoguse kohta (andmed Exceli tabelina võib alla laadida aadressilt http://www.emu.ee/~ktanel/bin_tunnuste_analyys/tudeng_ja_6lu.xlsx).

Rakendame logistilist regressioonanalüüsi prognoosimaks meheks olemise tõenäosust nädalas keskmiselt tarbitava õllekoguse alusel.

Andmeid ja analüüsi tulemusi on illustreeritud järgneval joonisel (ringid vastavad erinevatele õllekogustele ja ringi suurus tudengite arvule, pidev must joon on logistilise regressioonivõrrandi graafik ning y-telg vastab meheks olemise tõenäosusele).
 

 

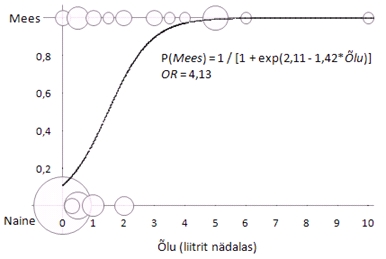
Nagu jooniselt näha, on naistudengite hulgas enim õlut mittejoovaid tudengeid, meestudengite tarbitavad õllekogused on suuremad, mistap on loomulik ka logistilise regressioonivõrrandi graafiku suund -- mida suurem on nädalas tarbitav õllekogus, seda suurema tõenäosusega on tegu meestudengiga.

Logistilise regressiooni võrrandi parameetrite hinnanguiks on: α = -2,11 ja β = 1,42. Seega on logistiline regressioonivõrrand esitatav kas joonisel toodud kujul (prognoosimaks meheks olemise tõenäosust)

p = P(Mees) = 1 / (1 + e^{2,11 - 1,42*Õlu})

või siis lineaarse võrrandina logaritmilise šansi tarvis kujul

ln[p/(1-p)] = -2,11 + 1,42*Õlu.

Šansside suhe avaldub kordaja β = 1,42 eksponentfunktsioonina: OR = e^1,42 = 4,13. Seega suurendab tudengite puhul ühe lisaliitri õlle joomine nädalas meheks olemise šanssi 4,13 korda võrreldes naiseks olemise šansiga.

 
Logistiline regressioon online-kalkulaatori abil:

• http://statpages.org/logistic.html