Fisheri täpne test

Fisheri täpne testi (ingl. Fisher exact test) abil kontrollitav hüpoteeside paar on analoogne χ²-testi hüpoteeside paariga:

H₀: tunnused on sõltumatud ehk potentsiaalne riskifaktor ei mõjuta uuritava sündmuse toimumist,
H₁: tunnused on sõltuvad ehk potentsiaalne riskifaktor mõjutab uuritava sündmuse toimumist;

aga tulemuseni jõudmise metoodika on erinev. Nimelt ei arvutata Fisheri täpse testi puhul teststatistiku väärtust, selle asemel leitakse kõik antud summaarsete rea- ja veerusageduste puhul võimalikud kahemõõtmelised sagedustabelid ning arvutatakse nende esinemise tõenäosused nullhüpoteesi eeldusel (tunnuste sõltumatue eeldusel). Et läbi mängitakse kõik võimalikud variandid, nimetatakse Fisheri täpset testi (ja tegelikult ka teisi kõigi võimalike variantide läbimängimisel baseeruvaid teste) permutatsioonitestiks. Tunnuste sõltumatue eeldusel on tõenäosus, et uuritavad indiviidid/objektid on tabeli latrite vahel jaotunud just mingil konkreetsel viisil, leitav hüpergeomeetrilisest jaotusest.

Üldjuhul avaldub mingi konkreetse mxk-sagedustabeli esinemise tõenäosus hüpergeomeetrilise jaotuse tõenäosusfunktsioonist kujul

,

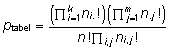kus n! = nx(n-1)x…x2x1 on n-i faktoriaal (definitsiooni kohselt on ka 0! = 1).

2x2-tabelite puhul avaldub konkreetse, fikseeritud rea- ja veerusummadega, tabeli tõenäosus kujul

p_tabel = [(a+b)!(c+d)!(a+c)!(b+d)!] / [n!a!b!c!d!].

Otsuse vastuvõtmiseks vajaliku olulisuse tõenäosuse arvutamiseks on Fisheri täpse testi puhul kaks võimalust:

• summeeritakse andmetele vastava sagedustabeli ja kõigi sellest väiksema esinemis-tõenäosusega tabelite tõenäosused;
• summeeritakse andmetele vastava sagedustabeli ja sellest nö samas suunas ekstreemsemate tabelite esinemistõenäosused ja korrutatakse tulemus kahega.

Koerte näite puhul on algne andmetele vastav sagedustabel kujul

	Ei saanud terveks	Sai terveks	Kokku
Emane	9	4	13
Isane	2	10	12
Kokku	11	14	25

ja sellise tabeli saamise tõenäosus soo ja ravi tulemuses sõltumatuse korral on p_tabel = [(10+2)!(4+9)!(10+4)!(2+9)!] / [25!10!2!4!9!] = 0,01059.

Alternatiivsed samade rea- ja veerusummadega sagedustabelid ning nende esinemise tõenäosused nullhüpoteesi eeldusel on järgmised (andmetele vastavast tabelist veel ebatõenäolisemad tabelid ja nende tõenäosused on esitatud paksus kirjas, andmetele vastavast tabelis nö samas suunas ekstreemsemate tabelite tõenäosused on täiendavalt allajoonitud):

11	2
0	12

p_tabel = 0,0000175

10	3
1	1

p_tabel = 0,00077

8	5
3	9

p_tabel = 0,06352

7	6
4	8

p_tabel = 0,19056

6	7
5	7

p_tabel = 0,26679

5	8
6	6

p_tabel = 0,30490

4	9
7	5

p_tabel = 0,12704

3	10
8	4

p_tabel = 0,03176

2	11
9	3

p_tabel = 0,00385

1	12
10	2

p_tabel = 0,000192

0	13
11	1

p_tabel = 0,00000269

Olulisuse tõenäosuse väärtuseks tuleb sõltuvalt arvutamismeetodist
p = 2×(0,01059+0,00077+0,0000175) = 0,02275
või
p = (0,01059+0,00077+0,0000175) + (0,00385+0,000192+0,00000269) = 0,01542.

Mõlemal viisil arvutatud p-väärtuse alusel võib lugeda tõestatuks alternatiivse hüpoteesi: ravi tulemus on soospetsiifiline (ehk seos ravi tulemuse ja koera soo vahel on statistiliselt oluline).

Valik online-kalkulaatoreid, mis pakuvad Fisheri täpse testi teostamise võimalust (enamasti vaid 2x2-tabeli tarvis):

• http://www.physics.csbsju.edu/stats/fisher.form.html
• http://vassarstats.net/ -> Frequency data
• http://www.quantitativeskills.com/sisa/statistics/fishrhlp.htm, http://www.quantitativeskills.com/sisa/statistics/fiveby2.htm
• http://www.langsrud.com/fisher.htm
• http://statpages.org/ctab2x2.html (lisaks väga palju erinevaid karakteristikuid)