Isa mudelist leitud geneetiliste parameetrite hinnangute täpsusest

Isa mudeli lihtsus, mis on peamine põhjus, miks seda mudelit lisaks isade aretusväärtuste hindamisele küllaltki laialdaselt ka uuritava tunnuse geneetilist determineeritust terves populatsioonis kirjeldava päritavuskoefitsiendi hindamiseks kasutatakse (eriti juhul, kui tegu on uudse näitajaga ja/või populatsiooniga/tõuga), annab võimaluse uurida ka erinevate katseplaanide/andmestruktuuride mõju geneetiliste parameetrite hinnangute täpsusele.

Statistilise mudeli parameetri hinnangu täpsust näitab see, kui vähe leitud hinnang varieerub. Varieeruvust kirjeldatakse enamasti hinnangu standardhälbega (või hinnangu standardhälbe hinnanguga, mis on defineeritud kui standardviga). Näiteks päritavuskoefitsiendi hinnangu täpsust mõõdab suurus 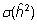(või ).
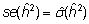Mudelist leitud prognooside täpsust mõõdab keskmine ruutviga (mean square error, MSE) või ruutjuur viimasest, mille hinnangut sageli (näiteks statistikaprogrammide väljatrükkides) ka lihtsalt standardveaks nimetatakse. Näiteks isa mudelist leitud j. isa mõju hinnangu täpsust mõõdab suurus .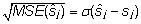

Hoolimata isa mudeli lihtsusest, on selle abil leitud parameetrite hinnangute standardvigade matemaatilised avaldised suhteliselt keerukad. Siiski on arvuti abil võimalik läbi viia modelleerimiseksperimente, uurimaks erinevate andmestruktuuride mõju hinnangute täpsusele, ja leida ka optimaalne tütarde arv isa kohta ette antud vaatluste arvu ja päritavuskoefitsiendi väärtuse korral.

Olles fikseerinud tulevase andmestiku suuruse N ja oletatava päritavuskoefitsiendi väärtuse h², on optimaalne tütarde arv isa kohta isade aretusväärtuste hindamise soovi korral esitatav valemiga

,

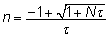(9)

kus .

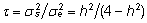Soovides aga isa mudelist hinnata võimalikult täpselt päritavuskoefitsienti, tuleks andmestiku moodustamisel võtta iga isa järglaste arvuks

,

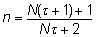(10)

Näide. Soovitakse uurida lehmade söödakasutuse efektiivsuse geneetilist determineeritust Eesti tingimustes. Raha on eraldatud nii palju, et sellest piisab 400 looma pidevaks jälgimiseks, mõõtmiseks ja katsete läbi viimiseks. Kui mitmelt isalt ja kui palju peaks võtma katsesse tütreid, et hinnata päritavuskoefitsienti võimalikult täpselt?

Planeeritav andmestiku suurus N = 400. Teades teiste maade teadlaste uuringuist, et huvipakkuva päritavuskoefitsiendi väärtus on ligikaudu 0,4, saame optimaalseks tütarde arvuks isa kohta vastavalt valemile (10)

.

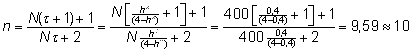Seega oleks uuritava tunnuse päritavuskoefitsiendi hindamiseks vaatlusaluses karjas/populatsioonis antud ajahetkel mõistlik valida välja N/n = 400/10 = 40 pulli igaüks 10 tütrega.

Kui nüüd aga lugeda päritavuskoefitsiendi väärtus teadaolevaks ja püstitada küsimus nii: kui mitu tütart peaks igalt pullilt analüüsima, saamaks võimalikult täpseid hinnanguid pullide aretusväärtustele? Vastuse saame leida valemist (9):

.

Et ette antud loomade arv 400 52-ga täpselt ei jagu, siis tuleks võtta uuringusse 8 pulli igaüks 50 tütrega.

Joonistel 1 ja 2 on kujutatud vastavalt isa mõju (pool isa aretusväärtusest) ja päritavuskoefitsiendi hinnangute täpsus (mõõdetuna hinnangu standardhälbena) sõltuvalt päritavuskoefitsiendi väärtusest ja tütarde arvust isa kohta fikseeritud andmestiku suuruse korral.

• Osutub, et mida väiksem on uuritava tunnuse aditiivgeneetiline determineeritus (st, et mida väiksem on päritavuskoefitsiendi väärtus), seda suuremat tütarde arvu isa kohta on vaja.
  
• Päritavuskoefitsiendi hindamiseks on vaja pigem suurt hulka isasid väiksema arvu tütardega.
  
• Aretusväärtuste hindamiseks on vaja jällegi suuremat hulka tütreid.

Viimased seosed on muidugi loomulikud, sest päritavuskoefitsiendi väärtus sõltubki eelkõige isade erinevusest -- mida enam isasid, seda paremini on võimalik erinevus tuvastatav, samas kui isa aretusväärtus sõltub tema tütarde keskmisest fenotüübiväärtusest -- mida enam tütreid, seda täpsemalt on nende keskmine fenotüübiväärtus hinnatav.

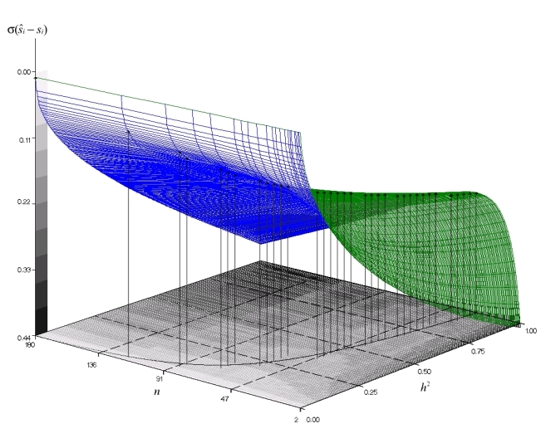
Joonis 1. Isa mõju hinnangu täpsus (mõõdetuna keskmise prognoosiveana 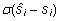) sõltuvalt järglaste arvust ja päritavuskoefitsiendi väärtusest vaatluste arvu N = 360 korral. Pidev joon xy-tasandil märgib optimaalset tütarde arvu isa kohta pideval ja vertikaalsed jooned diskreetsel skaalal.

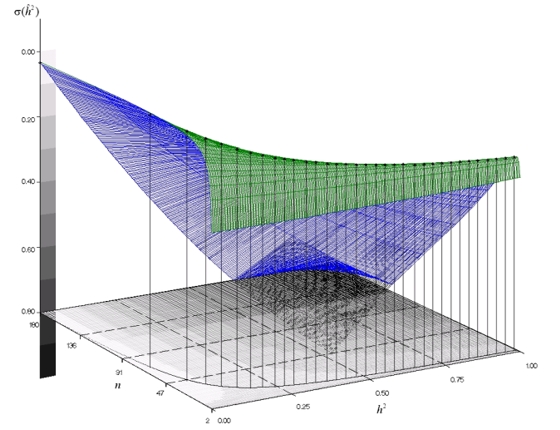
Joonis 2. Päritavuskoefitsiendi hinnangu täpsus (mõõdetuna hinnangu standardhälbena 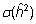) sõltuvalt järglaste arvust ja tegelikust päritavuskoefitsiendi väärtusest vaatluste arvu N = 360 korral. Pidev joon xy-tasandil märgib optimaalset tütarde arvu isa kohta pideval ja vertikaalsed jooned diskreetsel skaalal.